Апроксимација у Екцелу

Међу различитим методама предвиђања, не можемо помоћи изолацији апроксимације. Уз помоћ можете направити приближне прорачуне и израчунати планиране индикаторе, заменом првих објеката једноставним. У Екцел-у постоји и могућност коришћења овог метода за прогнозирање и анализу. Погледајмо како се ова метода може имплементирати у наведеном програму са уграђеним алатима.

Садржај

Извршење апроксимације
Питања и одговори

Извршење апроксимације

Име ове методе долази од латинске ријечи прокима - "најближе" То је апроксимација поједностављивањем и поравнавањем познатих индикатора, усклађивањем њих у тренду и њена основа. Али овај метод се може користити не само за прогнозирање већ и за истраживање већ доступних резултата. На крају крајева, апроксимација је заправо поједностављење оригиналних података, а поједностављена верзија је лакша за истраживање.

Главни алат који се користи за извршавање анти-алиасинг у Екцел-у јесте изградња линије трендова. Доња линија је да, на основу већ доступних индикатора, завршава се функција распореда за будуће периоде. Главна сврха линије тренда, како није тешко погодити, је припрема прогноза или идентификација општег тренда.

Али може се конструисати користећи једну од пет типова апроксимације:

Линеар;
Експоненцијални;
Логаритамски;
Полиномиал;
Снага.

Да размотримо сваку од опција детаљније одвојено.

Лекција: Како изградити линију трендова у Екцелу

Метод 1: линеарно помјерање

Пре свега, размотримо најједноставнију верзију апроксимације, наиме уз помоћ линеарне функције. Овде ћемо детаљније да се бавимо, јер ћемо објаснити опште тренутке карактеристичне за друге методе, наиме, конструкцију графикона и неке друге нијансе на којима се нећемо задржавати на наредним верзијама.

Пре свега, конструишемо график на основу којег ћемо извршити процедуру поравнавања. За скицирање графикона, узмимо таблицу у којој се јединични трошак јединице коју произведе предузеће и одговарајуће добити у датом периоду приказује месечно. Графичка функција коју ћемо конструисати одражаваће зависност повећања профита на смањење трошкова производње.

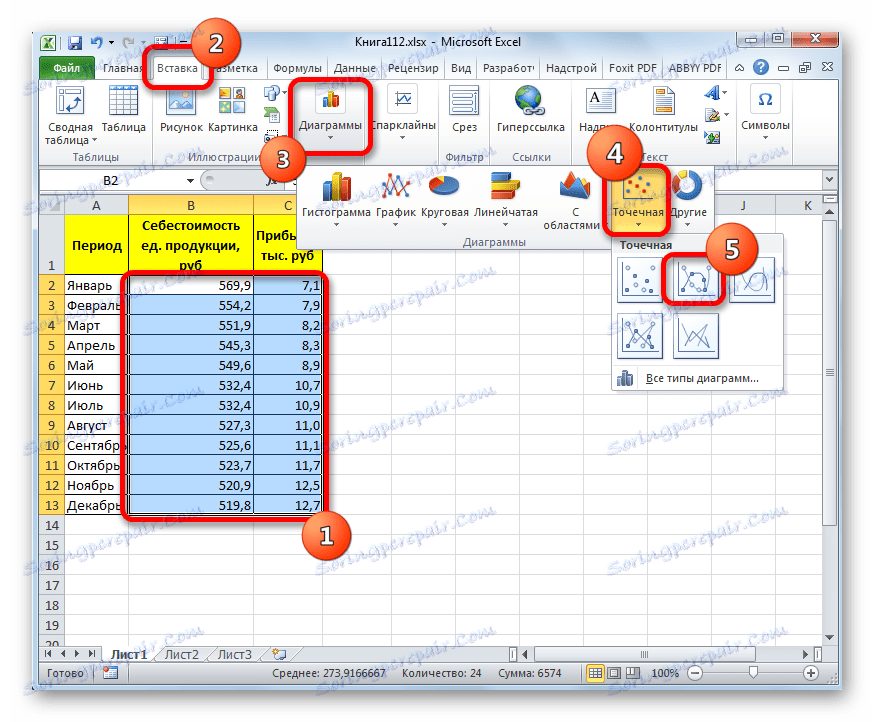
За плотирање графикона, пре свега, изаберемо колоне "Јединични трошкови производње" и "Профит" . После тога, пређите на картицу "Убаци" . Затим кликните на дугме "Спот" у пољу "Диаграмс". На отвореној листи изаберите назив "Спот са глатким кривинама и маркерима" . Овакве дијаграме су најприкладније за рад са линијом трендова, а самим тим и за примјену методе апроксимације у Екцел.

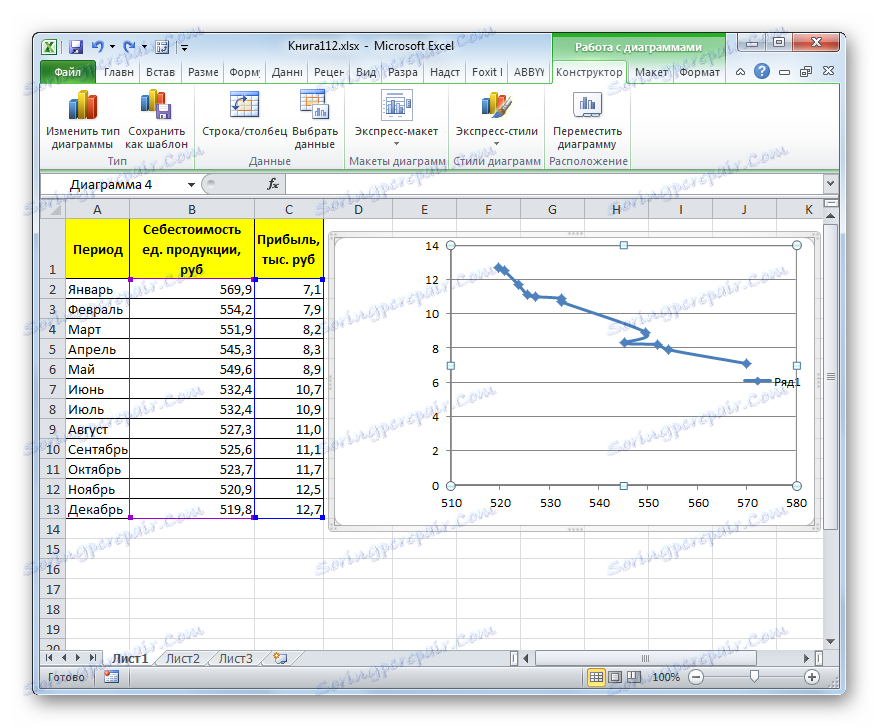
Графикон је изграђен.

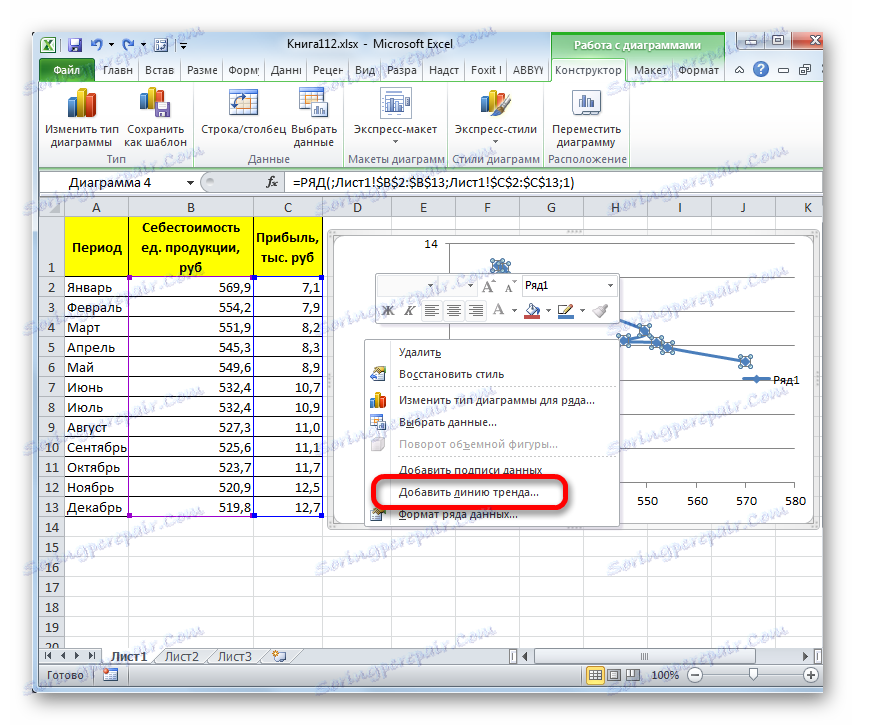
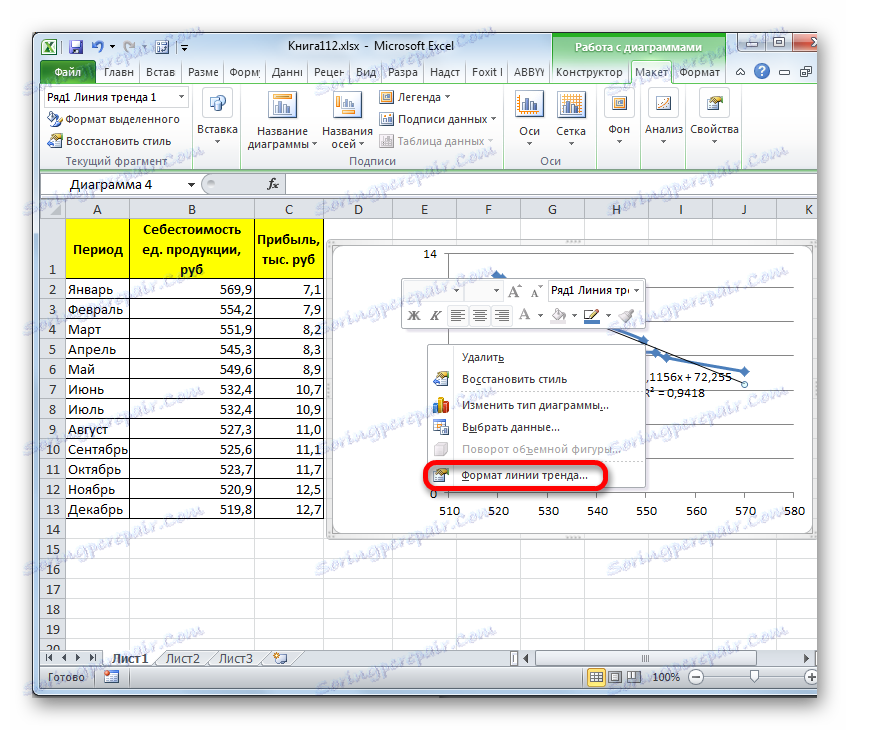
Да бисте додали линију трендова, изаберите је тако што ћете кликнути на десно дугме миша. Појавиће се контекст мени. Изаберите ставку "Додај линију тренда ..." у њему .
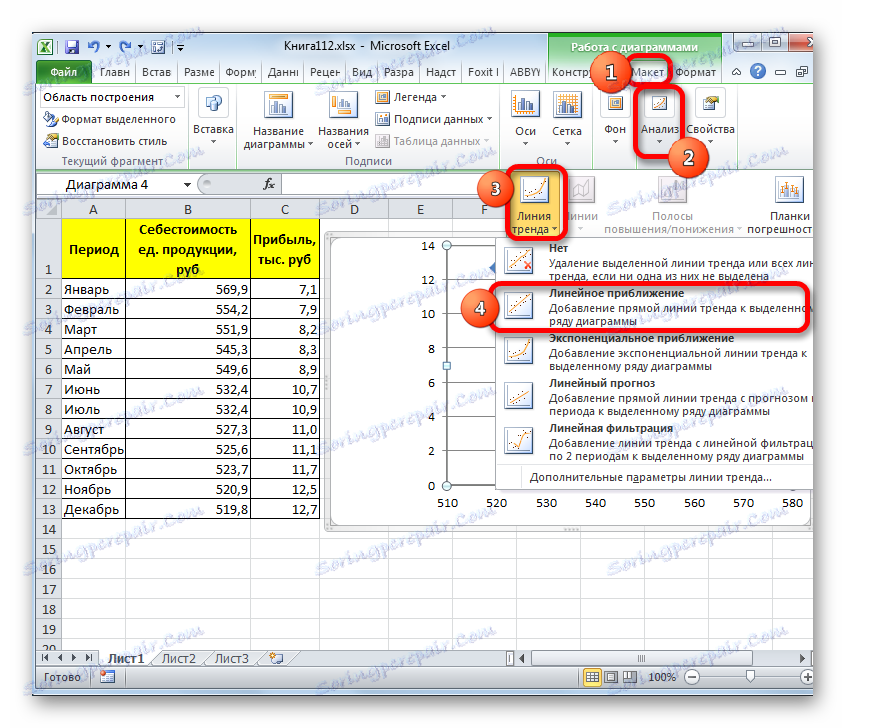
Постоји и други начин да га додате. У додатној групи табова на траци "Рад са графиконима" прелазимо на картицу "Лаиоут" . Затим, у пољу за анализу "Анализа" кликните на дугме "Тренд Лине" . Отвара се листа. Пошто треба да применимо линеарну апроксимацију, онда из презентованих позиција изаберемо "Линеарно апроксимацију" .

Ако сте изабрали прву опцију са додатком преко контекстног менија, отвориће се прозор за формат.
У блок параметру "Изградња линије тренда (апроксимација и анти-алиасинг)" поставите прекидач на позицију "Линија" .
Ако желите, можете да проверите положај "Приказ једначине на графикону" . Након тога, у дијаграму ће бити приказана једначина функције глајења.
Такође у нашем случају, у циљу упоређивања различитих варијанти апроксимације, важно је провјерити "Место на дијаграму вриједност поуздане апроксимације (Р ^ 2)" . Овај индикатор може варирати од 0 до 1 . Што је веће, боље је апроксимација (поузданија). Сматра се да са вредношћу овог индекса од 0,85 и више, глатко се може сматрати поузданим и ако је индикатор мањи, онда то није.

Након што извршите сва горе наведена подешавања. Кликните на дугме "Затвори" који се налази на дну прозора.

Као што видите, линија тренда је изграђена на графикону. За линеарну апроксимацију, означава се црном равном линијом. Ова врста глајења се може користити у најједноставнијим случајевима, када се подаци брзо мењају, а зависност вриједности функције на аргументу је очигледна.

Глаткост, која се користи у овом случају, описана је следећом формулом:

y=ax+b

У нашем конкретном случају, формула има следећи облик:

y=-0,1156x+72,255

Вредност поузданости апроксимације у нашој земљи је 0.9418 , што је прилично прихватљив резултат, који карактерише поравнање, као поуздан.

Метод 2: експоненцијална апроксимација

Сада погледајмо експоненцијални тип апроксимације у Екцелу.

Да бисте променили врсту линије трендова, изаберите је тако што ћете кликнути десним тастером миша и одаберите "Трендлине формат ..." у отвореном менију.

После тога покренут је прозор формата који нам је већ познат. У блоку селекције типа апроксимације, поставите прекидач у положај "Експоненцијални" . Остала подешавања остају иста као у првом случају. Кликом на дугме "Затвори" .

Након тога линија тренда ће бити изграђена на графикону. Као што видимо, приликом коришћења овог метода има нешто закривљени облик. Ниво поузданости је 0,9592 , што је више од коришћења линеарне апроксимације. Експоненцијални метод најбоље се користи када се прве вредности брзо мењају, а затим узимају уравнотежену форму.

Општи облик функција помицања је следећи:

y=be^x

где е је основа природног логаритма.

У нашем конкретном случају формула је узела следећи облик:

y=6282,7*e^(-0,012*x)

Метод 3: Логаритамско поравнање

Сада је време да се размотри метод логаритамске апроксимације.

На исти начин као у претходном времену кроз контекстни мени покрећемо прозор формата линије трендова. Поставите прекидач на положај "Логаритамски" и кликните на дугме "Затвори" .

Постоји поступак за изградњу линије тренда са логаритамском апроксимацијом. Као иу претходном случају, ова опција је боље користити када се у почетку подаци брзо мењају, а затим избалансирани изглед. Као што видите, ниво поузданости је 0,946. Ово је веће од коришћења линеарног метода, али ниже од квалитета линије трендова са експоненцијалним поравнањем.

У принципу, формула за изједначавање изгледа овако:

y=a*ln(x)+b

где је лн вредност природног логаритма. Отуда име методе.

У нашем случају, формула има следећи облик:

y=-62,81ln(x)+404,96

Метод 4: Полномијално умиривање

Време је да се узме у обзир начин полимерног гладјења.

Прелазимо на прозор формата линије трендова, као што смо то учинили више од једном. У блоку "Изградња линије тренда" поставите прекидач у положај "Полином" . Десно од ове ставке је поље "Степен" . Ако изаберете "Полиномиал", он постаје активан. Овдје можете одредити било коју вриједност снаге од 2 (подразумевано постављено) на 6 . Овај индикатор одређује број максима и минима функције. Када се инсталира полином другог степена, описује се само један максимум, а када се подешава полином шестог степена, може се описати до пет максима. Прво, остављамо подразумевана подешавања, односно указујемо на други степен. Остала подешавања остају иста као што смо их ставили у претходне методе. Кликните на дугме "Затвори" .

Израђена је линија трендова помоћу ове методе. Као што видите, још је закривљено него експоненцијална апроксимација. Ниво поузданости је већи него код претходно коришћених метода и износи 0,9724 .
Овај метод се најуспешније примењује у случају да су подаци константно променљиви. Функција која описује ову врсту помицања изгледа овако:
y=a1+a1*x+a2*x^2+…+an*x^n

У нашем случају, формула је преузела облик:
y=0,0015*x^2-1,7202*x+507,01
Сада, променимо степен полинома да видимо да ли ће се резултати разликовати. Враћамо се у прозор формата. Тип апроксимације је остављен полином, али испред њега у степенском прозору постављамо максималну могућу вредност - 6 .

Као што видите, након тога је наша линија тренда имала облику изразите криве, у којој је број максима шест. Ниво поузданости се повећао још више, достигавши 0.9844 .

Формула која описује ову врсту поравнања узима се у следећем облику:

y=8E-08x^6-0,0003x^5+0,3725x^4-269,33x^3+109525x^2-2E+07x+2E+09

Метод 5: Постепено изравнавање

На крају, размотрите метод приближавања снаге у Екцелу.

Прелазимо на прозор "Тренд Лине Формат" . Пребацивање типа помицања подесите на позицију "Снага" . Приказујући једначину и ниво поузданости, као и увек, ми их остављамо. Кликните на дугме "Затвори" .

Програм обликује линију трендова. Као што видимо, у нашем случају то је линија са благим кривинама. Степен поверења је 0.9618 , што је прилично висок показатељ. Од свих горе наведених метода, степен поузданости био је већи само када се користи метода полинома.

Овај метод се ефикасно користи у случајевима интензивне промене података о функцијама. Важно је узети у обзир да је ова варијанта примјењива само под условом да функција и аргумент не узимају негативне или нулте вриједности.

Општа формула која описује овај метод је следећа:

y=bx^n

У нашем конкретном случају изгледа овако:

y = 6E+18x^(-6,512)

Као што видимо, коришћењем специфичних података које смо користили за примјер, највиши ниво поузданости показао је методом полиномске апроксимације са полиномом у шестој моћи ( 0.9844 ), што је најнижи ниво поузданости у линеарној методи ( 0.9418 ). Али то не значи да ће се иста тенденција користити при коришћењу других примера. Не, ниво ефикасности наведених метода може се значајно разликовати, у зависности од специфичног типа функције за коју ће бити изграђена линија трендова. Према томе, ако је одабрана метода најефикаснија за ову функцију, то не значи да ће у другој ситуацији бити оптимална.

Ако не можете одмах да утврдите, на основу горе наведених препорука, која врста апроксимације је исправна за вас, онда је смисла провести све методе. Након изградње линије трендова и гледања нивоа поузданости, можете одабрати најбољу опцију.