Екцел

Коришћење кластер анализе у Мицрософт Екцелу

Један од алата за решавање економских проблема је кластер анализа. Користећи га, кластери и други објекти у низу података класификују се у групе. Овај метод се може користити у Екцелу. Да видимо како се то ради у пракси.

Употреба кластер анализе

Уз помоћ кластерске анализе, могуће је узорковати на основу онога што се истражује. Његов главни задатак је поделити вишедимензионални низ у хомогене групе. Као критеријум груписања, коефицијент корелације пара или евклидско растојање између објеката се примењује према датом параметру. Вредности које су најближе једни другима су груписане заједно.

Иако се најчешће ова врста анализе користи у економији, може се користити и за биологију (за класификацију животиња), за психологију, медицину и многе друге области људске активности. Анализа кластера може се примијенити помоћу стандардног Екцел алата за ове сврхе.

Пример употребе

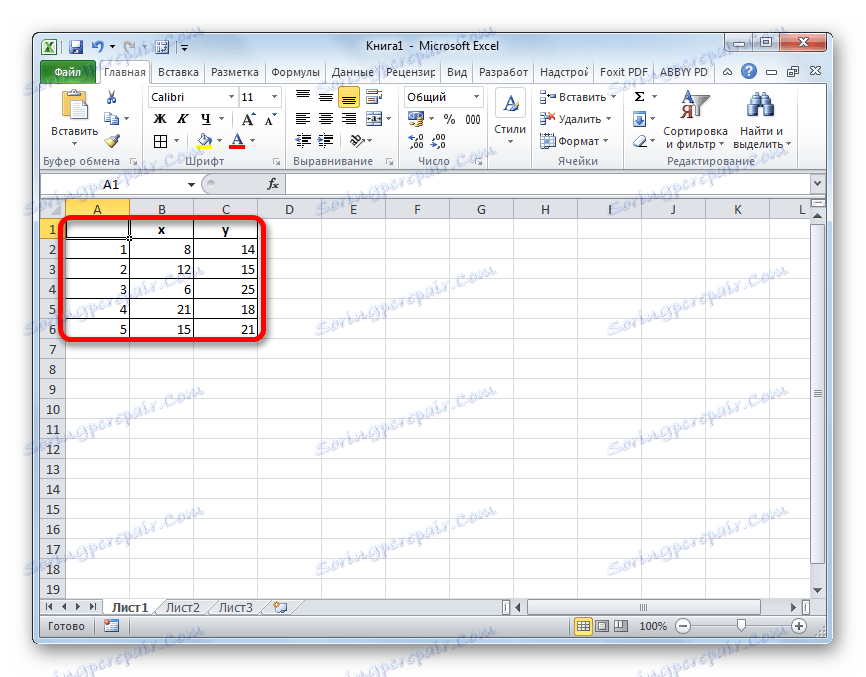
Имамо пет објеката који карактеришу два проучавана параметра - к и и .

  1. На ове вредности применити формулу евклидског растојања, која се израчунава из шаблона:

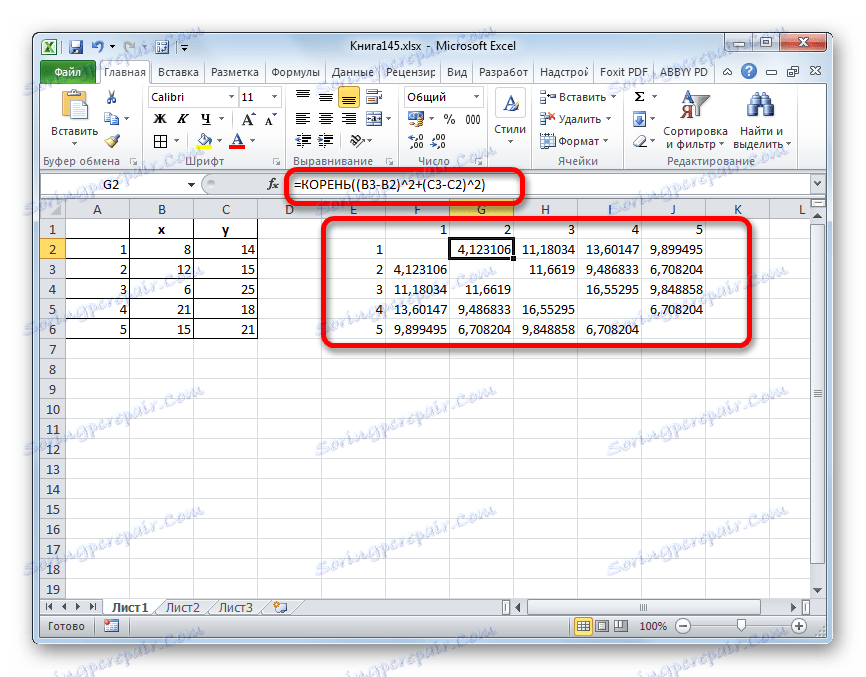
    =КОРЕНЬ((x2-x1)^2+(y2-y1)^2)

    2. Научени објекти у програму Мицрософт Екцел

  2. Ова вриједност се израчунава између сваког од пет објеката. Резултати израчунавања смештени су у матрицу удаљености.

    3. Матрица растојања у Мицрософт Екцелу

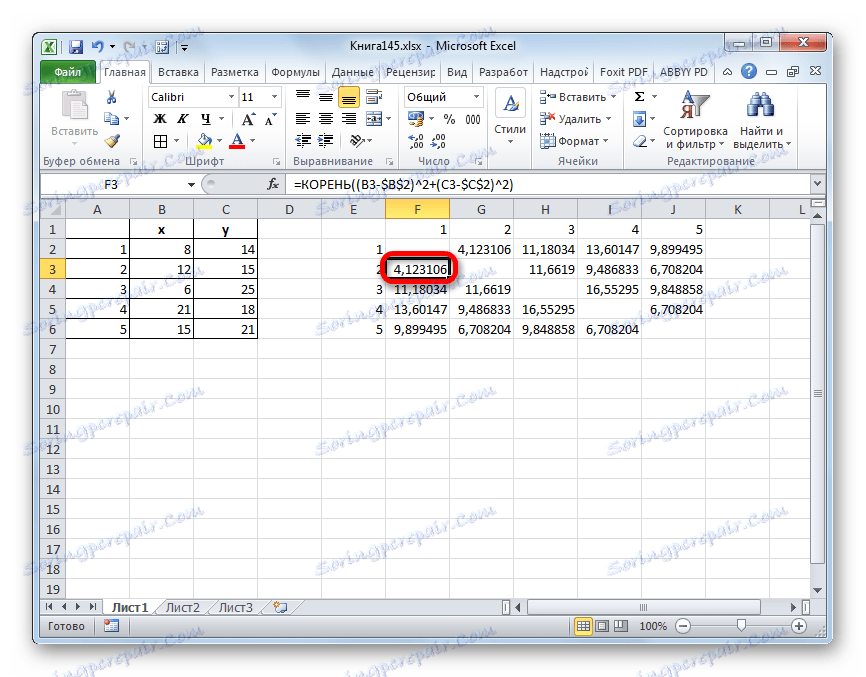
  3. Изгледамо, између којих вриједности је најмање растојање. У нашем примеру, ово су објекти 1 и 2 . Раздаљина између њих је 4.123106, што је мање од било којих других елемената дате популације.

    4. Растојање између објеката је минимално у Мицрософт Екцелу

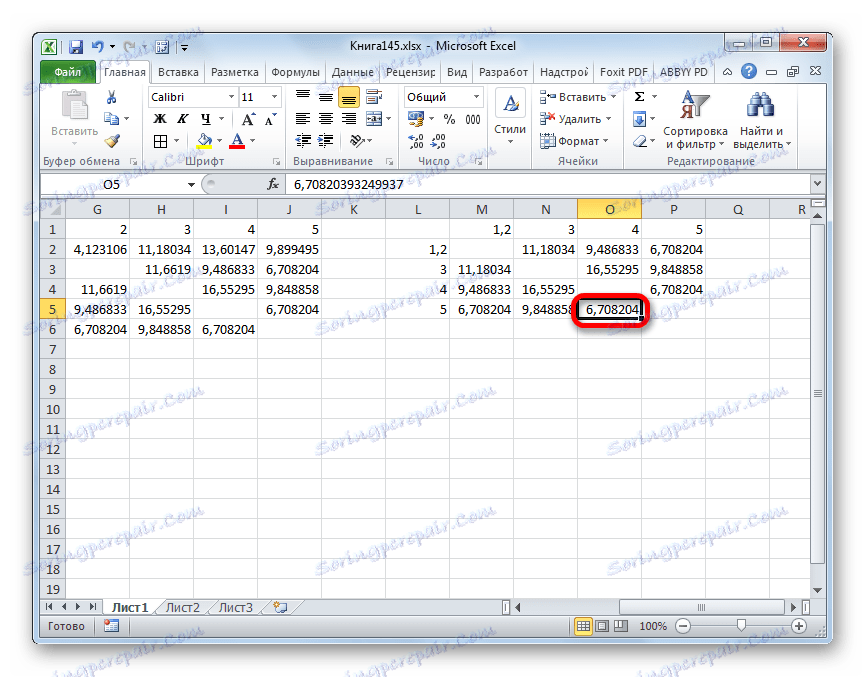
  4. Ми комбинирамо ове податке у групу и формирамо нову матрицу, у којој вриједности 1,2 су посебан елемент. Када компонујемо матрицу, остављамо најмању вриједност из претходне табеле за комбиновани елемент. Поново гледамо, између којих елемената је растојање минимално. Овај пут је 4 и 5 , а такође и објект 5 и група објеката 1,2 . Растојање је 6,708204.

    5. Растојање између објеката је минимално у другој матрици у Мицрософт Екцелу

  5. Додамо наведене елементе у општи кластер. Ми формирамо нову матрицу на исти принцип као и раније. То јест, тражимо најниже вриједности. Дакле, видимо да се наш скуп података може поделити у два кластера. У првом кластеру, најближи елементи су 1 , 2 , 4 , 5 . У другом кластеру, у нашем случају, само један елемент је представљен - 3 . Релативно је далеко од других објеката. Растојање између кластера је 9.84.

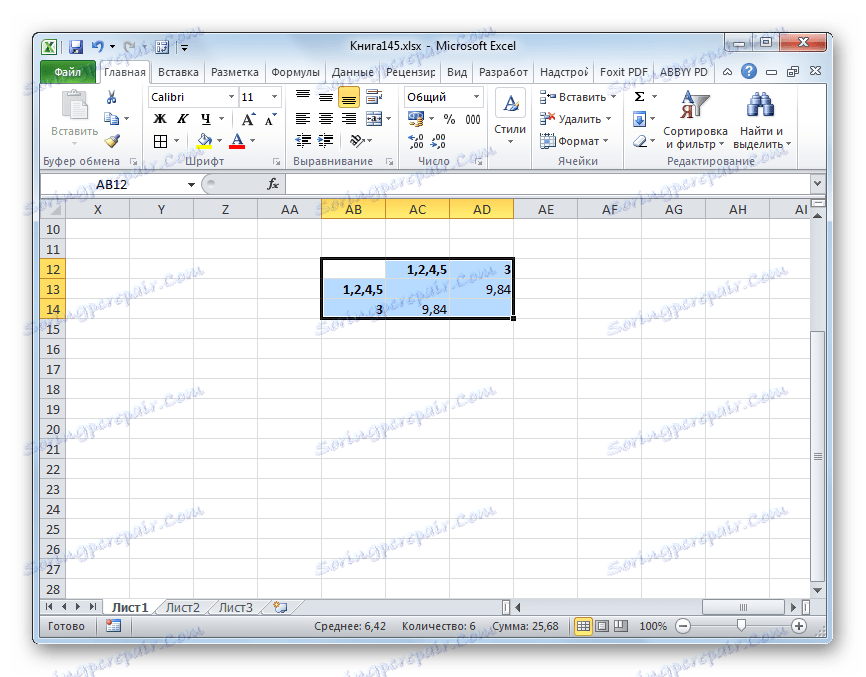
Укупна вредност у програму Мицрософт Екцел

Ово закључује процедуру за подјелу колекције у групе.

Као што можете видети, иако генерално, кластер анализа може изгледати као компликована процедура, није тако тешко разумјети нијансе ове методе. Најважније је разумјети основни образац групирања.