Решење система једначина у Мицрософт Екцелу

Способност решавања система једначина може често имати користи не само у учењу, већ иу пракси. У исто време, сваки корисник рачунара не зна да постоје сопствене варијанте решавања линеарних једначина у Екцелу. Хајде да сазнамо како изводити овај задатак помоћу различитих алата овог процесора таблице на различите начине.

Решења

Било која једначина може се сматрати решена само када се пронађу корени. У Екцел-у постоји неколико могућности за проналажење корена. Хајде да погледамо сваку од њих.

Метод 1: Матрични метод

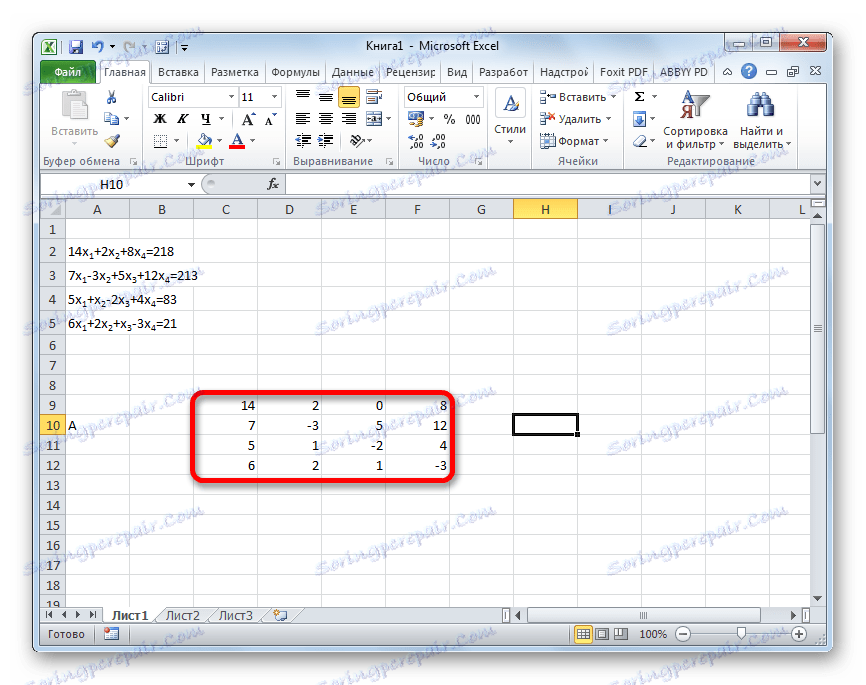
Најчешћи начин решавања система линеарних једначина са Екцел алатима је коришћење матричне методе. Састоји се из конструисања матрице коефицијената израза, а затим стварања инверзне матрице. Покушајмо да искористимо ову методу за решавање следећег система једначина:


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


1. Матрицу попуњавамо бројевима који су коефицијенти једначине. Ови бројеви морају бити уређени редоследом редом, узимајући у обзир локацију сваког корена на који одговарају. Ако у једном изразу недостаје један од корена, онда се у овом случају коефицијент сматра једнаком нули. Ако коефицијент није наведен у једначини, али је одговарајући корен присутан, онда се претпоставља да је коефицијент 1 . Добијену таблицу означимо као вектор А.
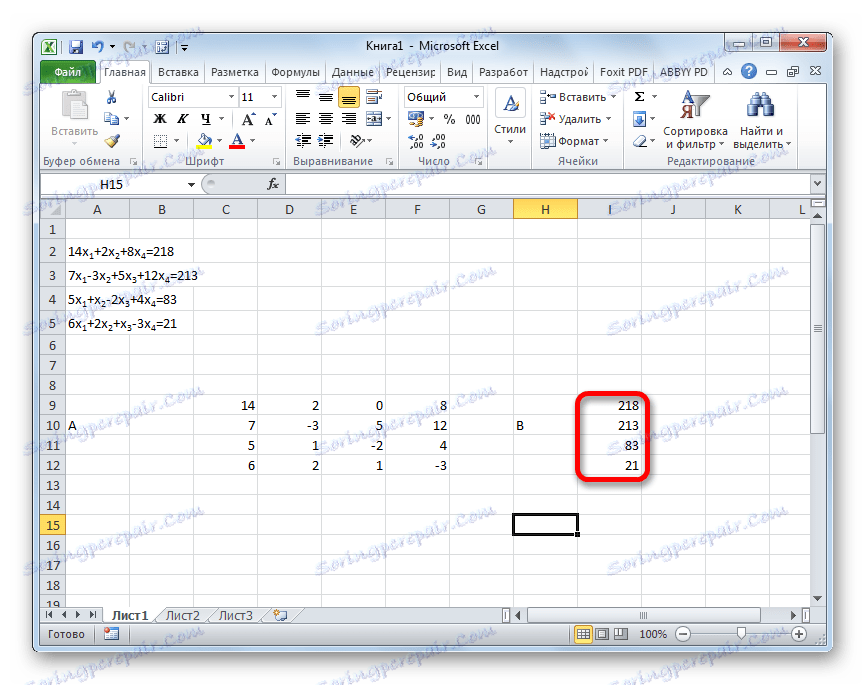
2. Одвојено напишите вредности након знака "једнако". Обележите их својим заједничким именом, као вектор Б.
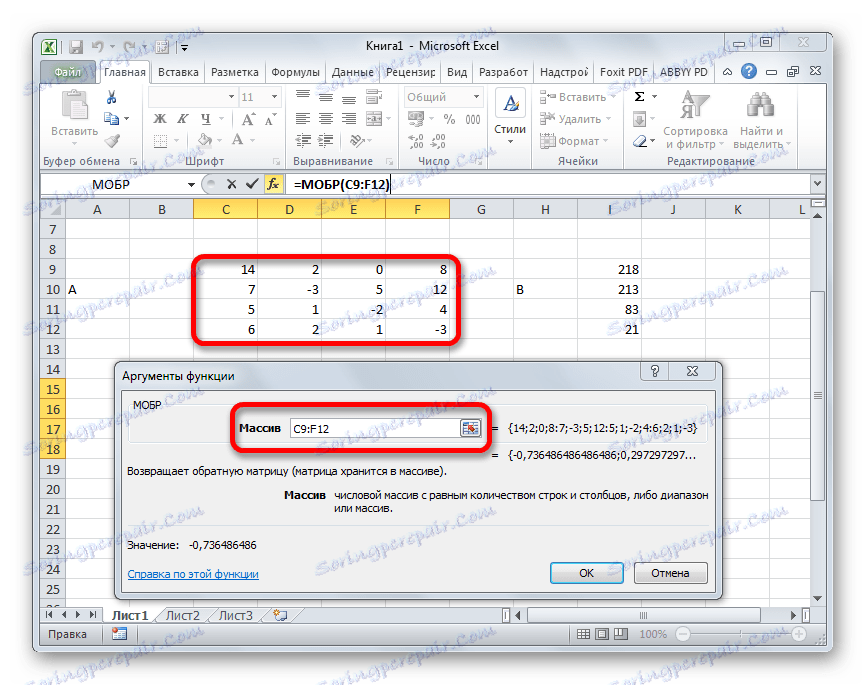
3. Пре свега, да би се пронашли корени једначине, морамо наћи инверзну матрицу постојеће. На срећу, Екцел има специјалног оператора, који је дизајниран да реши овај проблем. Зове се ИЦБМ . Има прилично једноставну синтаксу:

   =МОБР(массив)

   Аргумент "Арраи" је, заправо, адреса изворне таблице.

   Дакле, хајде да изаберемо регион празних ћелија на листу, који је једнак по величини у опсегу оригиналне матрице. Кликом на дугме "Убаци функцију" , налази се у близини линије формуле.

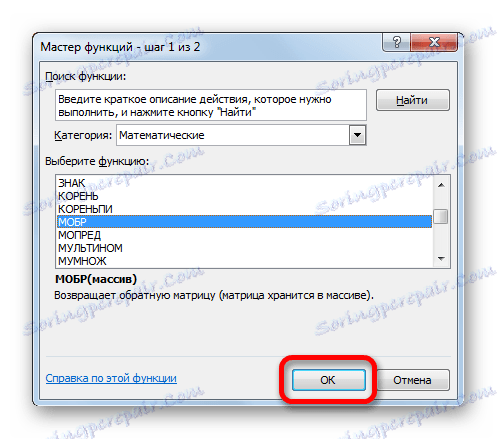
4. Стартује функционални чаробњак . Идемо у категорију "Математички" . На приказаној листи тражимо назив "МОБР" . Након што се пронађе, изаберите је и кликните на дугме "ОК" .
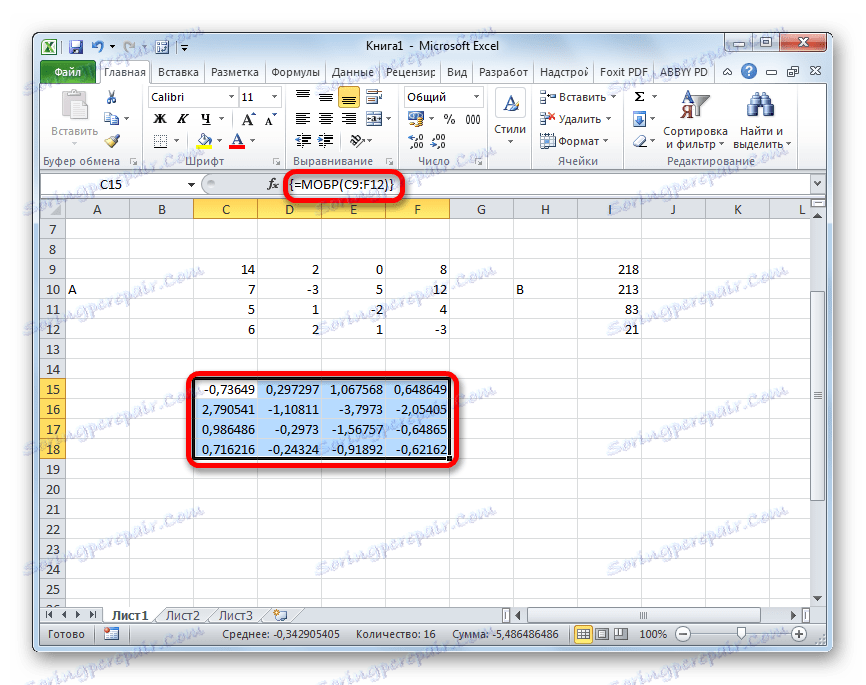
5. Покренут је прозор аргумента МОБР функције. Има само једно поље у броју аргумената - "Арраи" . Овде морате навести адресу наше табеле. За ову сврху поставили смо курсор у овом пољу. Затим држите леви тастер миша и изаберите област на листу где се налази матрица. Као што видите, подаци о координатама локације се аутоматски уносе у поље прозора. Након завршетка овог задатка, најочигледније је да кликнете на дугме "ОК" , али не пожурите. Чињеница је да је кликом на ово дугме једнако кориштењу наредбе Ентер . Али када радите са низовима након што довршите унос формуле, не би требало да кликнете на дугме Ентер , већ направите скуп пречица на тастатури Цтрл + Схифт + Ентер . Ову операцију обављамо.
6. Дакле, након тога, програм обавља прорачуне и на излазу у претходно додељеној области имамо реверсну матрицу за ово.
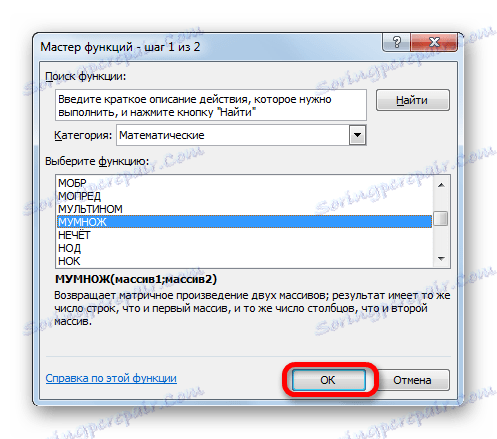
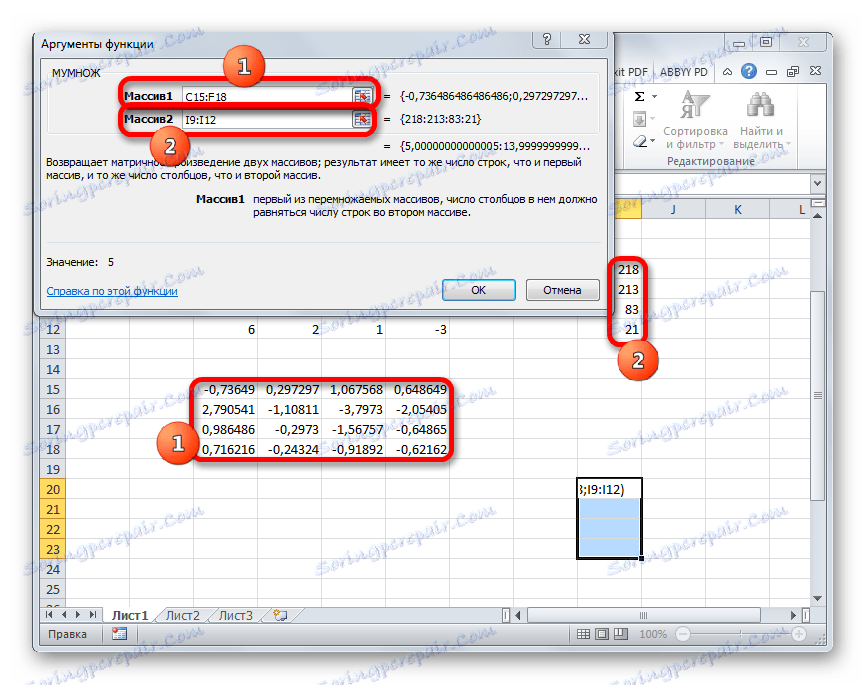
7. Сада морамо множити инверзну матрицу матрицом Б , која се састоји од једне колоне вриједности које се налазе након знака једнакости у изразима. За множење табела у Екцел-у постоји и одвојена функција, која се зове ХУМАН . Ова изјава има следећу синтаксу:

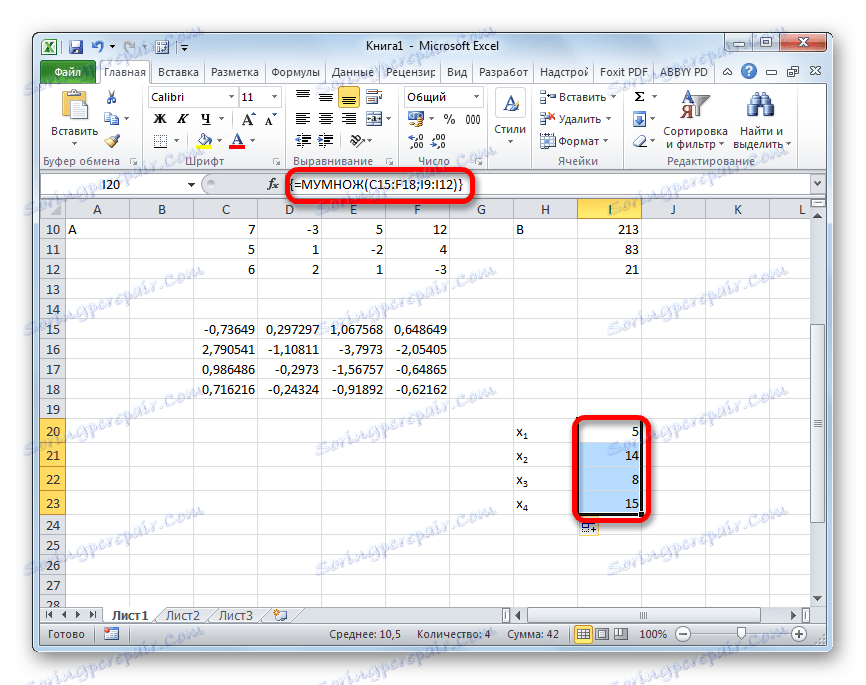
   =МУМНОЖ(Массив1;Массив2)

   Изаберемо опсег, у нашем случају који се састоји од четири ћелије. Затим поново покрените чаробњака функције кликом на икону "Инсерт фунцтион" .

8. У категорији "Матхематицал" , Стартед Визард оф фунцтионс , изаберите име "ХУМБЛЕ" и кликните на дугме "ОК" .
9. Прозор аргумената функције МУЛТИ . У пољу "Арраи1" уносимо координате наше инверзне матрице. За то, као и последњи пут, поставили смо курсор у поље и притиском лево дугме миша, изаберите одговарајућу табелу са курсором. Изводимо сличну акцију за унос координата у пољу "Арраи2" , само овај пут бирате вредности колоне Б. Након што се спроведу горе поменуте акције, опет не журим да притиснете дугме "ОК" или тастер Ентер и упишите Цтрл + Схифт + Ентер .
10. Након ове акције, корени једначине се приказују у претходно одабраној ћелији: Кс1 , Кс2 , Кс3 и Кс4 . Они ће бити уређени узастопно. Дакле, можемо рећи да смо решили овај систем. Да би се верификовала исправност решења, довољно је да се ти корени замене за оригинални систем израза. Ако се посматра једнакост, то значи да је приказани систем једначина исправно решен.

Лекција: Инверзна матрица у Екцелу

Метод 2: избор параметара

Друга позната метода решавања система једначина у Екцелу је примена методе селекције параметара. Суштина ове методе лежи у потрази за супротном. То је, на основу познатог резултата, тражимо непознати аргумент. Користимо квадратну једначину

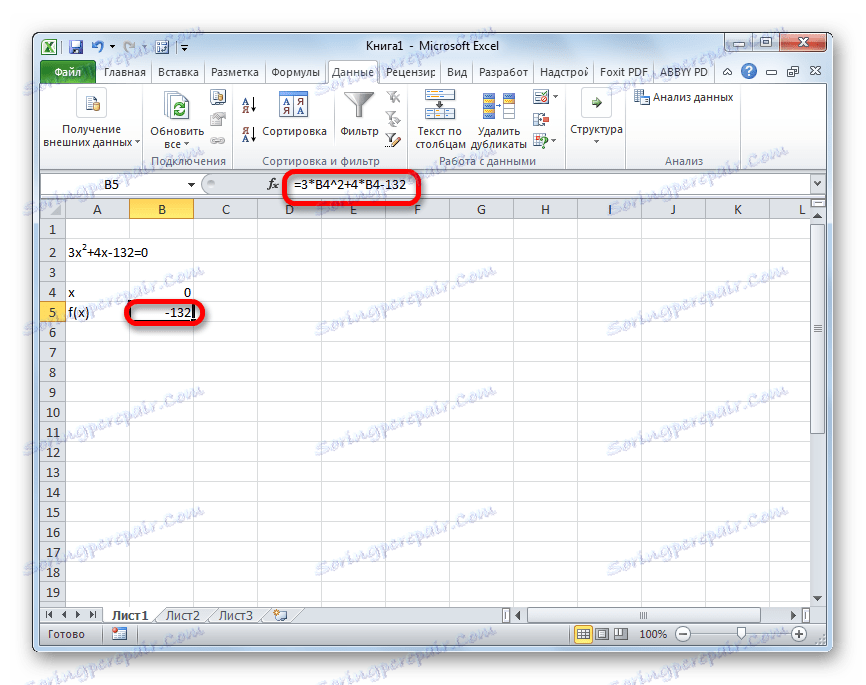
3x^2+4x-132=0

1. Претпоставимо вредност к за једнаку 0 . Израчунамо одговарајућу вредност ф (к) применом следеће формуле:

   =3*x^2+4*x-132

   Умјесто вриједности "Кс", замијените адресу ћелије гдје се налази број 0 , који смо узели за к .

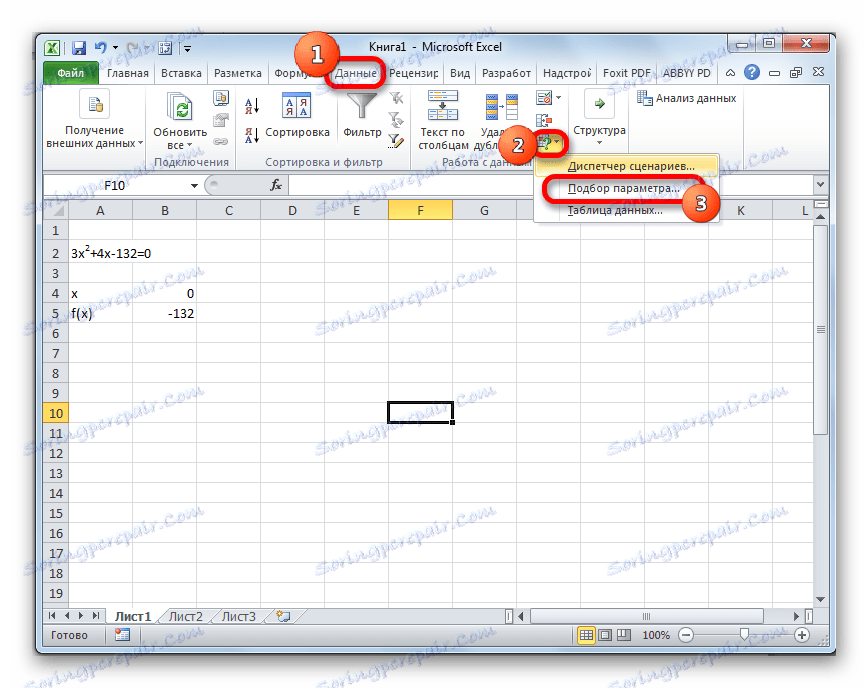
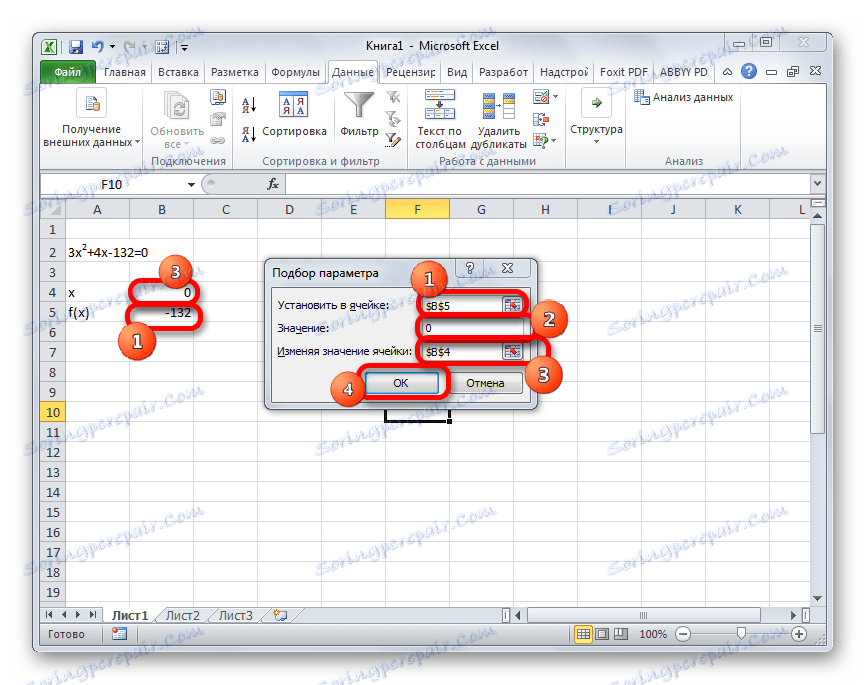
2. Идите на картицу "Подаци" . Кликните на дугме "Анализа шта ако" . Ово дугме налази се на траци у оквиру "Рад са подацима" . Приказује се падајућа листа. Изаберите ставку "Избор параметара ..." у њему .
3. Покреће се прозор за избор параметара. Као што видите, састоји се од три поља. У пољу "Подеси у ћелију" унесемо адресу ћелије у којој се пронађе формула ф (к) , израчуната од стране нас мало раније. У пољу "Вредност" унесите број "0" . У пољу "Промена вредности" уносимо адресу ћелије у којој се налази вриједност к , коју смо раније узели за 0 . Након што завршите ове кораке, кликните на дугме "ОК" .
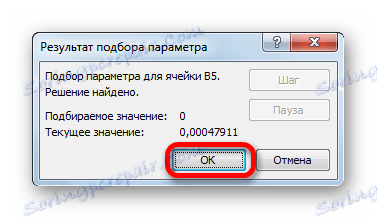
4. Након тога, Екцел изврши израчунавање одабиром параметра. Ово ће бити пријављено кроз информативни прозор који се појавио. У њему кликните на дугме "ОК" .
5. Резултат израчунавања корена једначине биће у ћелији коју смо доделили у пољу "Промена вредности" . У нашем случају, као што видимо, к ће бити једнако 6 .

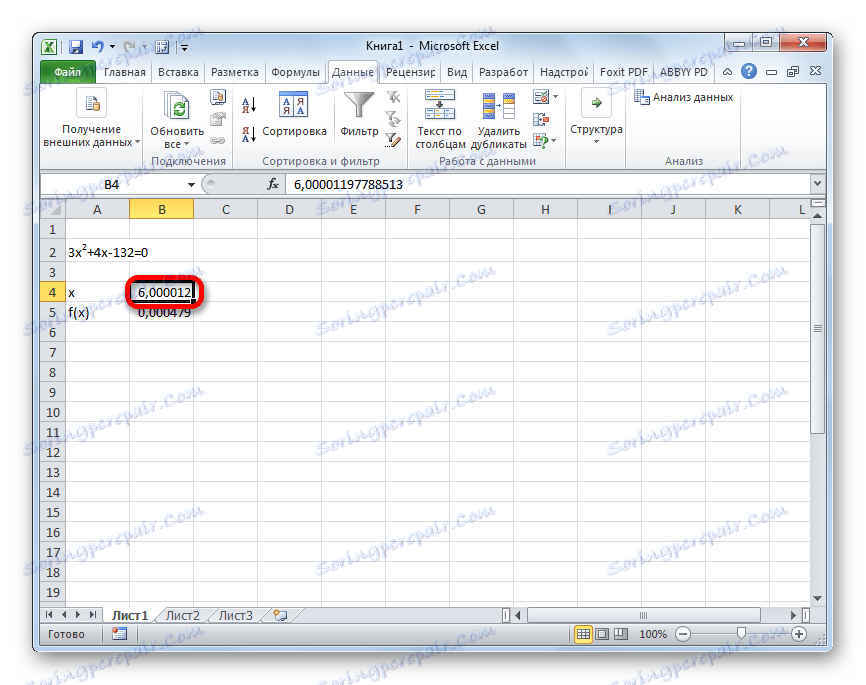
Овај резултат се такође може проверити замјеном ове вриједности у решеном изразу умјесто вриједности к .

Лекција: Избор параметара у Екцелу

Метод 3: Крамеров метод

Сада покушавамо да решимо систем једначина помоћу Црамеровог метода. На пример, узмите исти систем који је коришћен у Моду 1 :


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


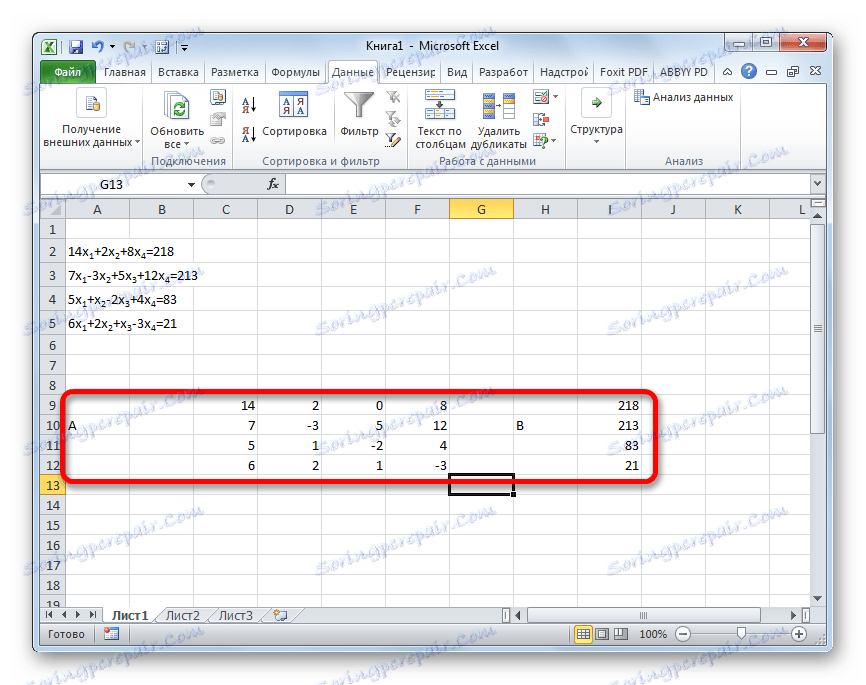
1. Као иу првом поступку, саставимо матрицу А из коефицијента једнаџби и табеле Б од вриједности које стоје за једнаким знаком.
2. Затим направимо још четири стола. Свака од њих је копија матрице А , само за ове копије једна колона се замјењује табелом Б. Прва табела има прву колону, друга табела има другу колону и тако даље.
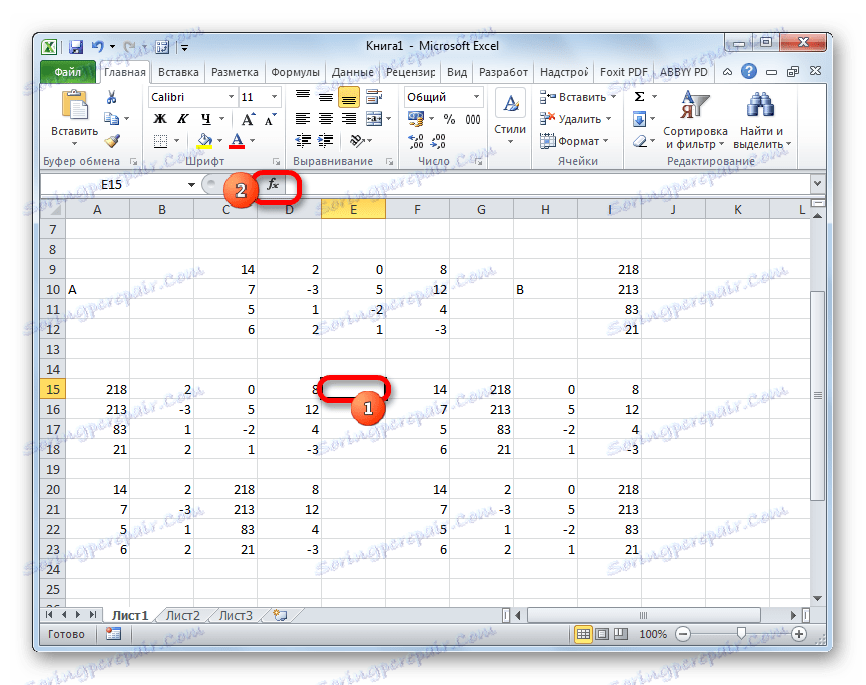
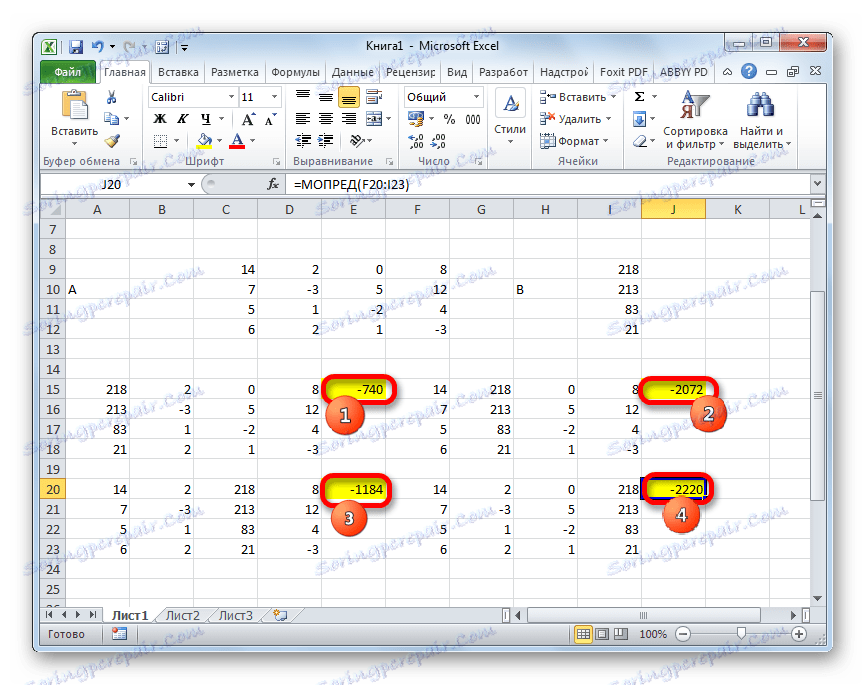
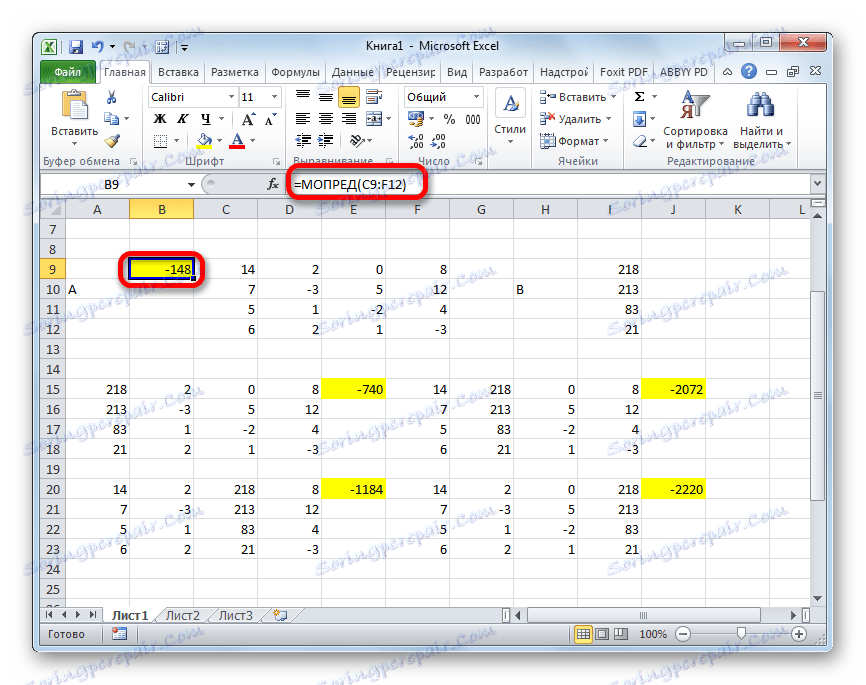
3. Сада морамо израчунати детерминанте за све ове табеле. Систем једначина ће имати решења само ако све детерминанте имају вредност другачију од нуле. Да би поново израчунали ову вредност у Екцел-у, постоји посебна функција - МОПРЕД . Синтакса овог оператора је:

   =МОПРЕД(массив)

   Тако, као иу случају МБД функције, једини аргумент је референца на табелу која се обрађује.

   Дакле, изаберите ћелију у којој ће се приказати детерминанта прве матрице. Затим кликните на дугме "Инсерт фунцтион" , која је позната из претходних метода.

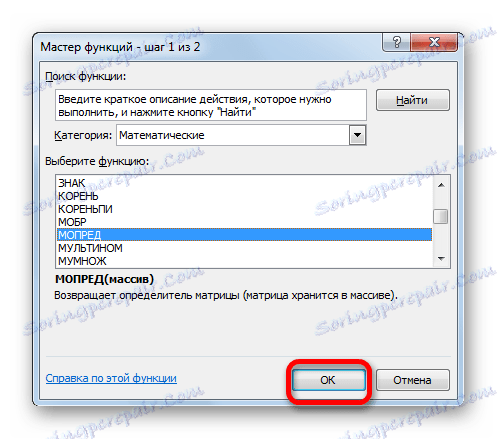
4. Прозор Визардс је активиран. Прелазимо на категорију "Математички", а међу листама оператора изаберемо име "МОПРЕД" . Након тога, кликните на дугме "ОК" .
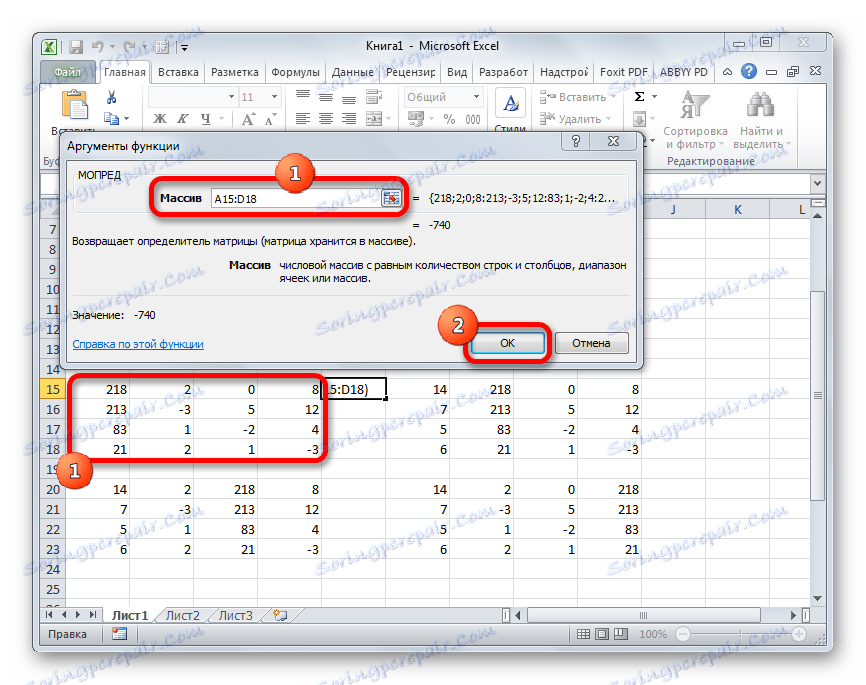
5. Покренут је прозор аргумената функције МОПЕД . Као што видите, има само једно поље - "Арраи" . У овом пољу уносимо адресу прве трансформисане матрице. Да бисте то урадили, поставите показивач у поље, а затим изаберите матрични опсег. Након тога, кликните на дугме "ОК" . Ова функција емитује резултат у једној ћелији, а не у низу, тако да не морате притиснути Цтрл + Схифт + Ентер да бисте израчунали.
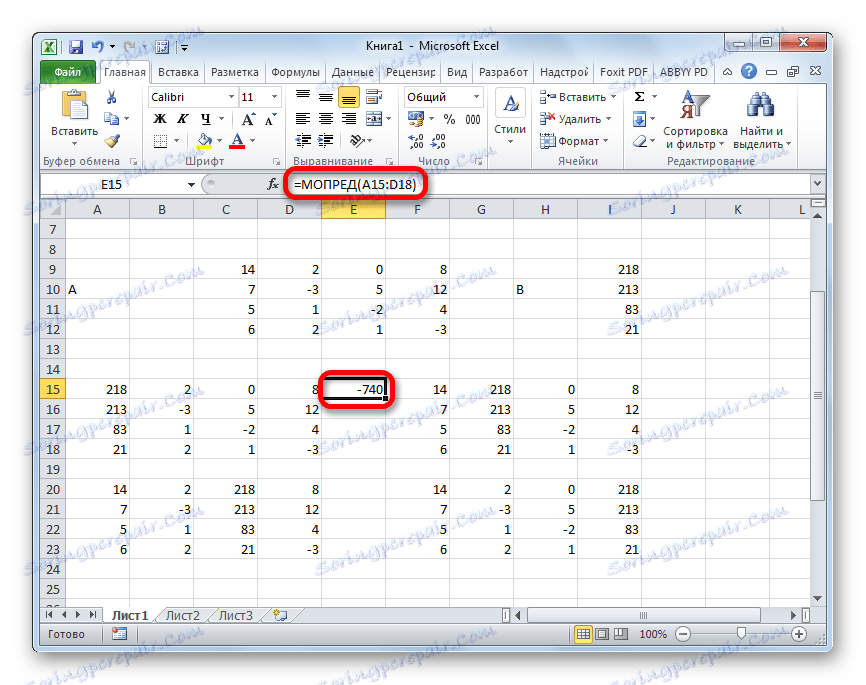
6. Функција израчунава резултат и излази у претходно одабрану ћелију. Као што можете видети, у нашем случају детерминанта је -740 , то јест, није једнака нули, што је погодно за нас.
7. Слично томе, израчунамо детерминанте за преостале три табеле.
8. У завршној фази израчунавамо детерминант примарне матрице. Поступак је исти за исти алгоритам. Као што видите, детерминанта примарне табеле је такође различита од нуле, па се матрица сматра неизгенерисана, тј. Систем једначина има решења.
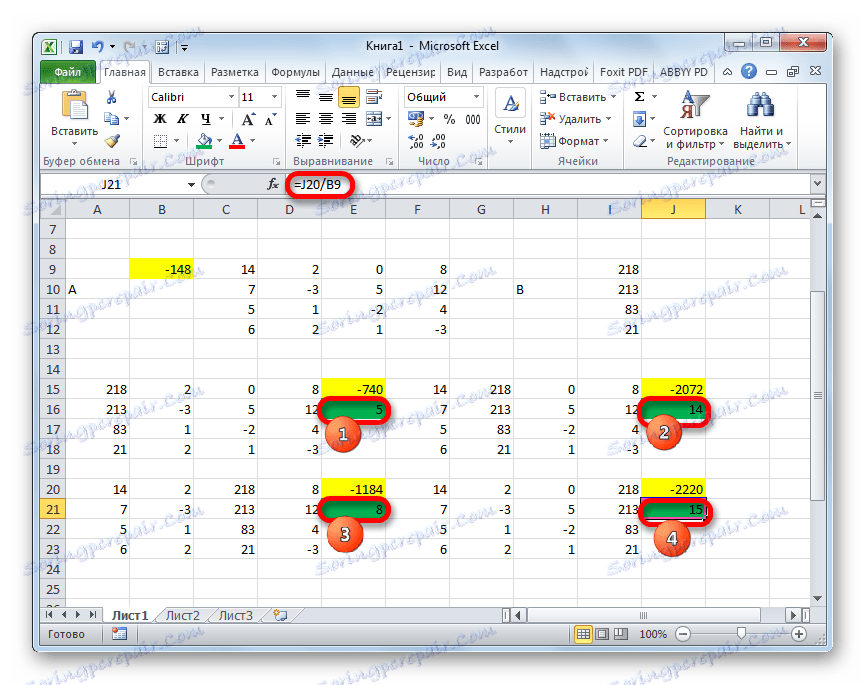
9. Сада је вријеме пронаћи корене једначине. Корен једначине ће бити једнак односу детерминанте одговарајуће трансформисане матрице до детерминанте примарне табеле. Дакле, након што смо поделили све четири детерминанте трансформисаних матрица један по један - 148 , што је детерминанта оригиналне табеле, добијамо четири корена. Као што видите, оне су једнаке вредности од 5 , 14 , 8 и 15 . Према томе, они се подударају са коренима које смо пронашли користећи инверзну матрицу у методу 1 , што потврђује исправност рјешења система једначина.

Метод 4: Метода Гаусса

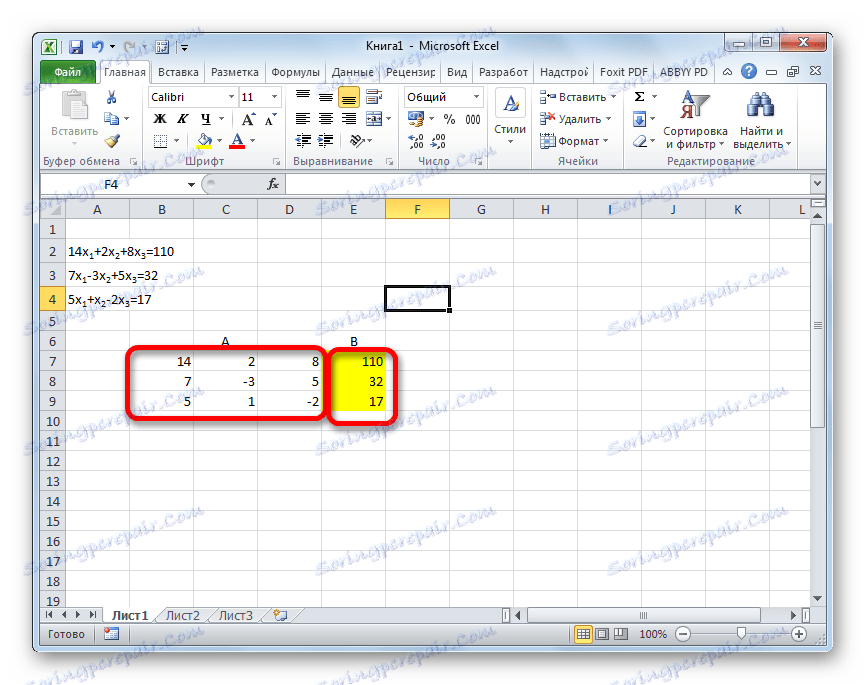
Решавање система једначина може се обавити и помоћу Гауссовог метода. На пример, узмимо једноставнији систем једначина три непознате:


14 x1 +2 x2 +8 x3 =110
7 x1 -3 x2 +5 x3 =32
5 x1 + x2 -2 x3 =17


1. Поново, заправо сакупљамо коефицијенте у табели А и слободне термине лоциране након знакова "једнако" у табели Б. Али овог пута ћемо заједно спојити обе табеле, јер ће нам то бити потребно у будућности. Важан услов је да се у првој ћелији матрице А вредност разликује од нуле. У супротном случају, треба редефинисати редове на местима.
2. Копирајте први ред две повезане матрице у низу испод (за јасноћу, можете прескочити једну линију). У првој ћелији која се налази у реду чак нижим од претходне, уносимо следећу формулу:

   =B8:E8-$B$7:$E$7*(B8/$B$7)

   Ако другачије уређујете матрице, онда ће се адресе ћелија формуле имати другачија вредност за вас, али можете их израчунати упоређивањем са формулама и сликама које су овде дате.

   Након уноса формуле, изаберите цео ред ћелија и притисните Цтрл + Схифт + Ентер . Формула низа ће бити примењена на ред и она ће бити испуњена вредностима. Тако смо се одузели од прве линије, помножени са односом првих коефицијената првих два израза система.

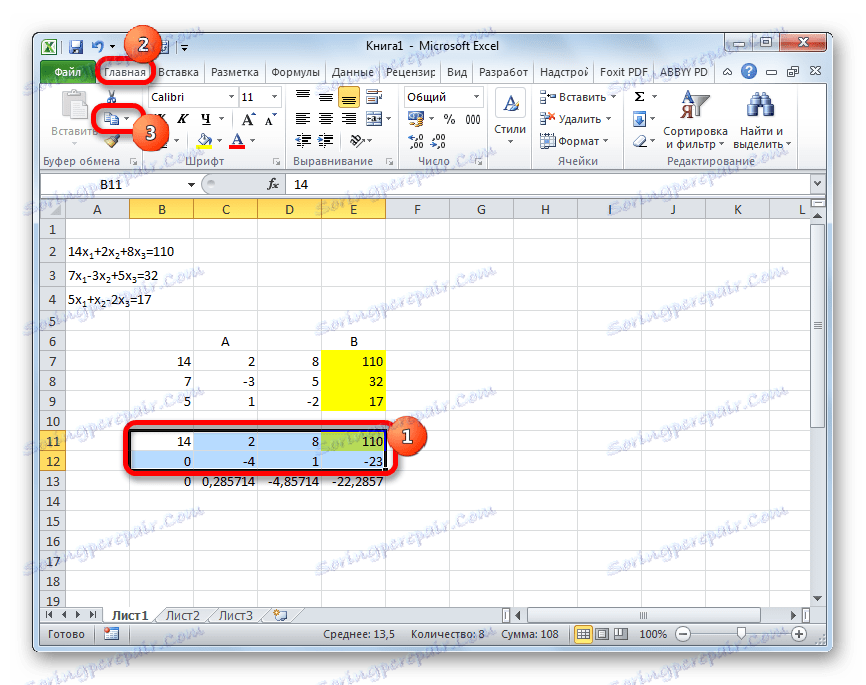
3. После тога копирајте резултирајућу линију и залепите је на линију испод.
4. Изаберите прве две линије након недостајуће линије. Кликните на дугме "Копирај" , који се налази на траци на картици "Почетна" .
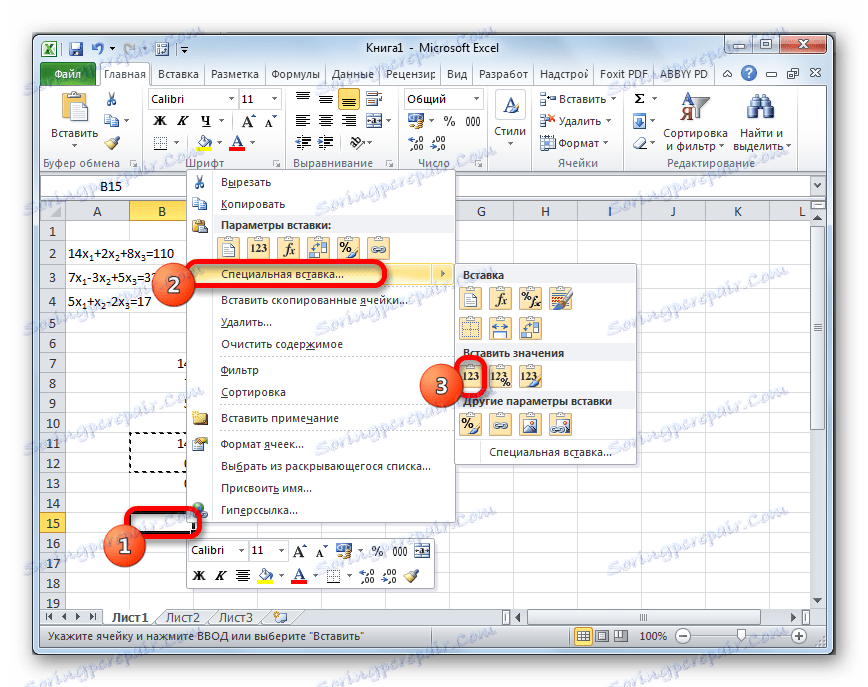
5. Пропуштамо линију након последњег записа на листу. Изаберите прву ћелију у следећој линији. Десни клик. У отвореном контекстном менију ми лебдимо курсор преко ставке "Посебно налепи" . На додатној листи која почиње, изаберите ставку "Вредности" .
6. У следећој линији унесите формулу поља. Одузима други ред из трећег реда претходне групе података, помножен са односом другог коефицијента трећег и другог реда. У нашем случају формула ће имати следећи облик:

   =B13:E13-$B$12:$E$12*(C13/$C$12)

   Након уношења формуле, изаберите читаву серију и примијените пречицу на тастатури Цтрл + Схифт + Ентер .

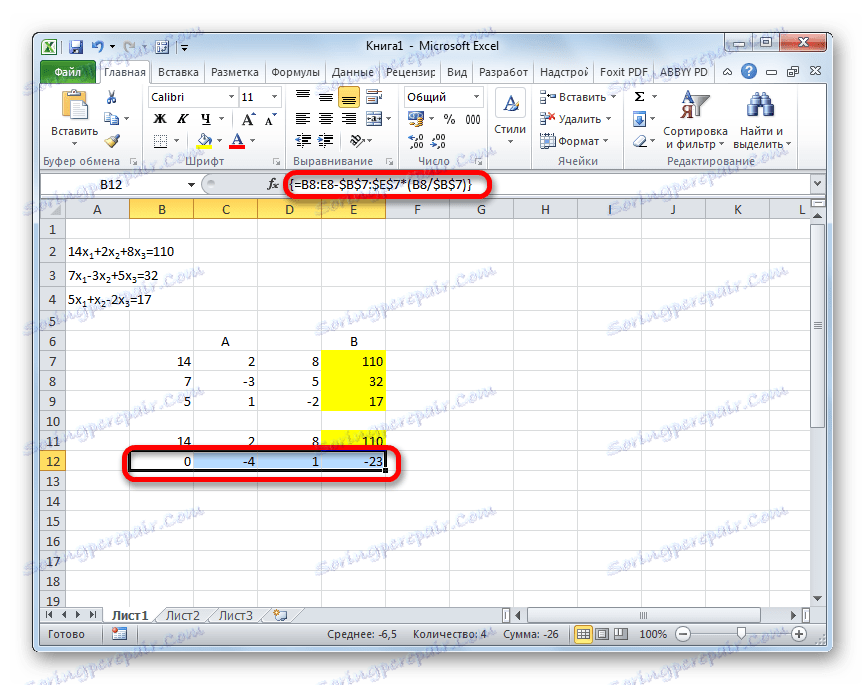
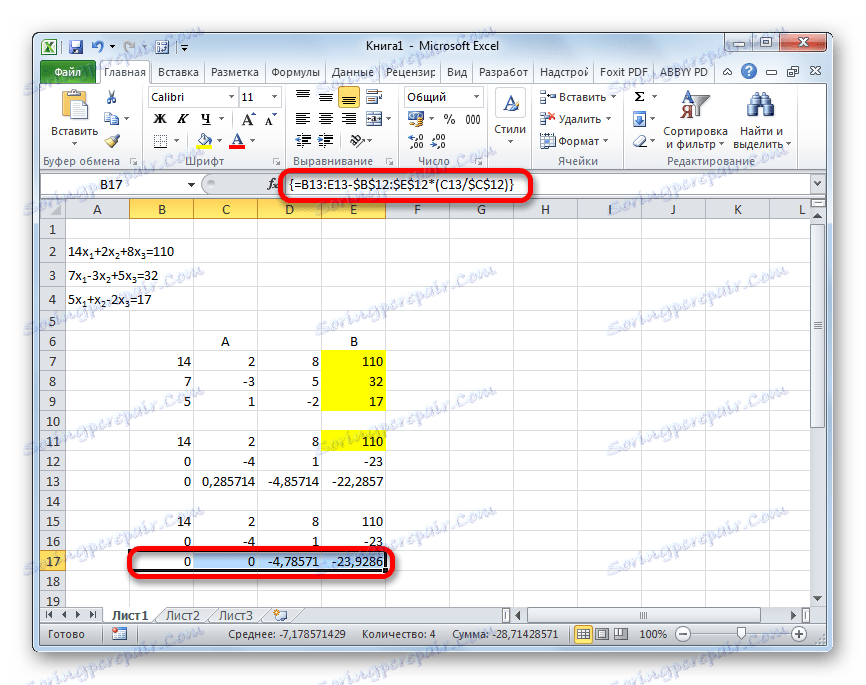
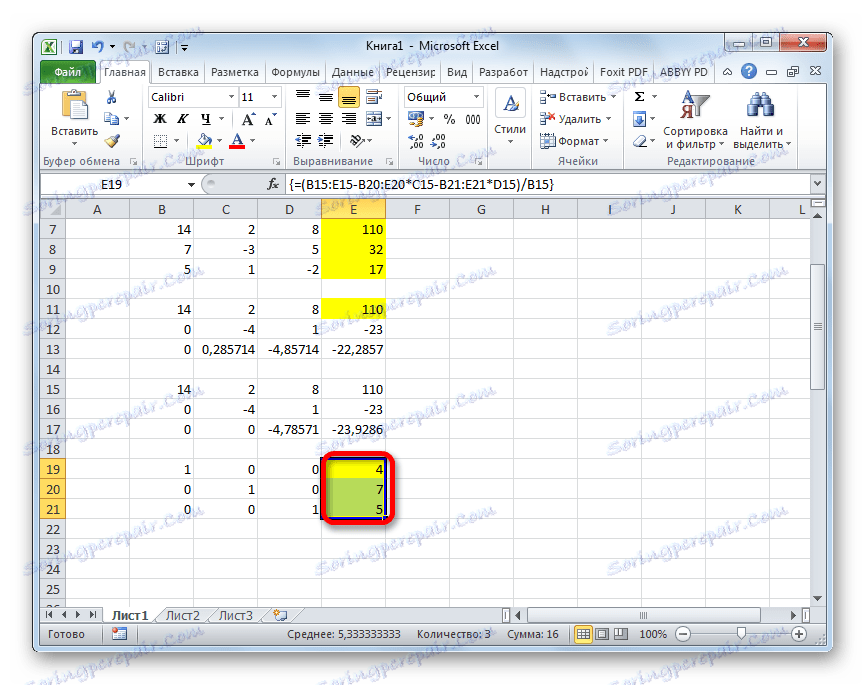
7. Сада је неопходно извршити обрнути рад користећи Гауссову методу. Прескакамо три реда из последњег записа. У четвртој линији уносимо формулу поља:

   =B17:E17/D17

   Дакле, поделимо последњу линију коју смо израчунали трећим коефицијентом. Након што унесете формулу, изаберите целу линију и притисните Цтрл + Схифт + Ентер .

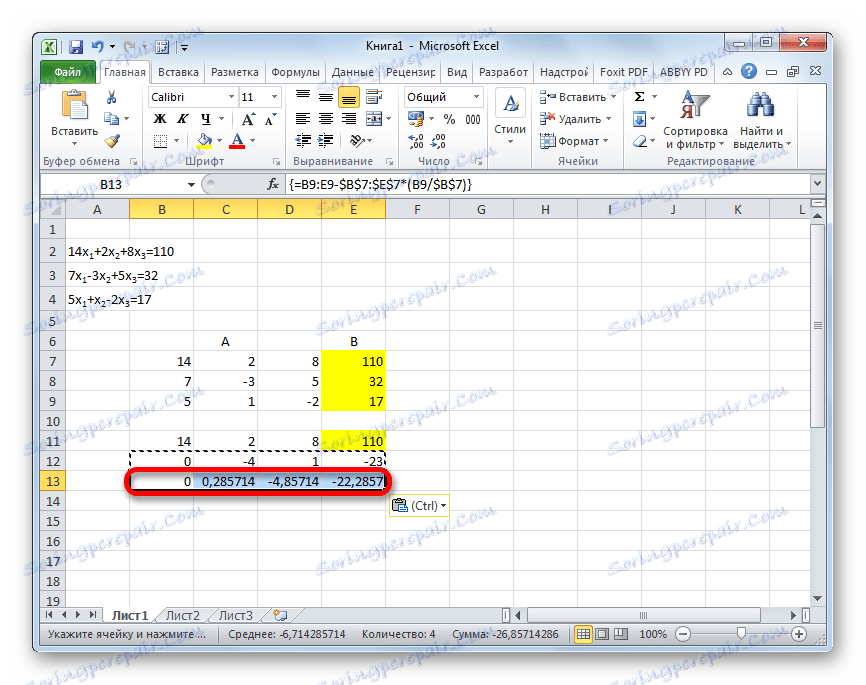
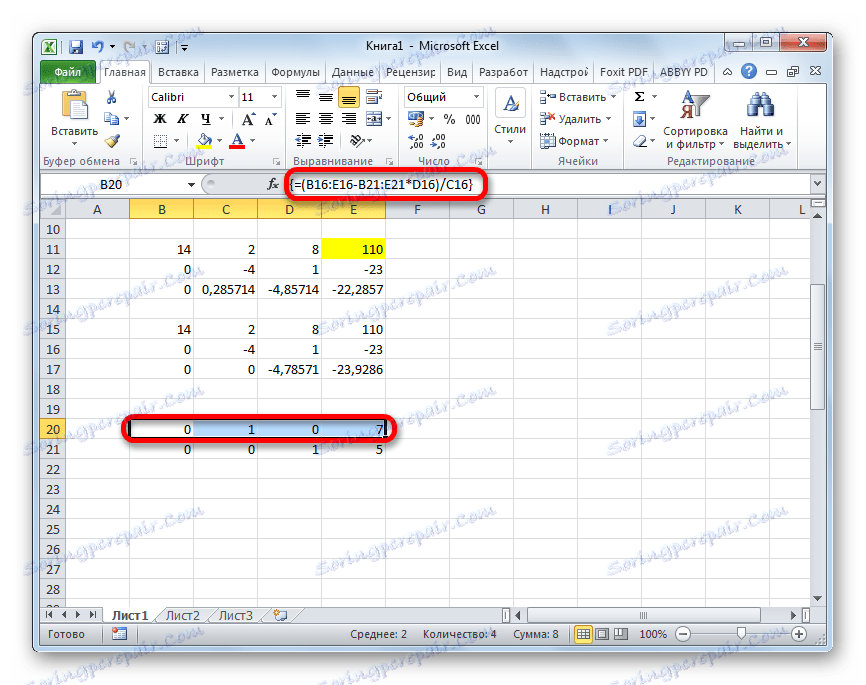
8. Уздигнемо се на линији према горе и уђемо у њу следећу формулу поља:

   =(B16:E16-B21:E21*D16)/C16

   Притиснемо уобичајену комбинацију тастера за примену формуле низа.

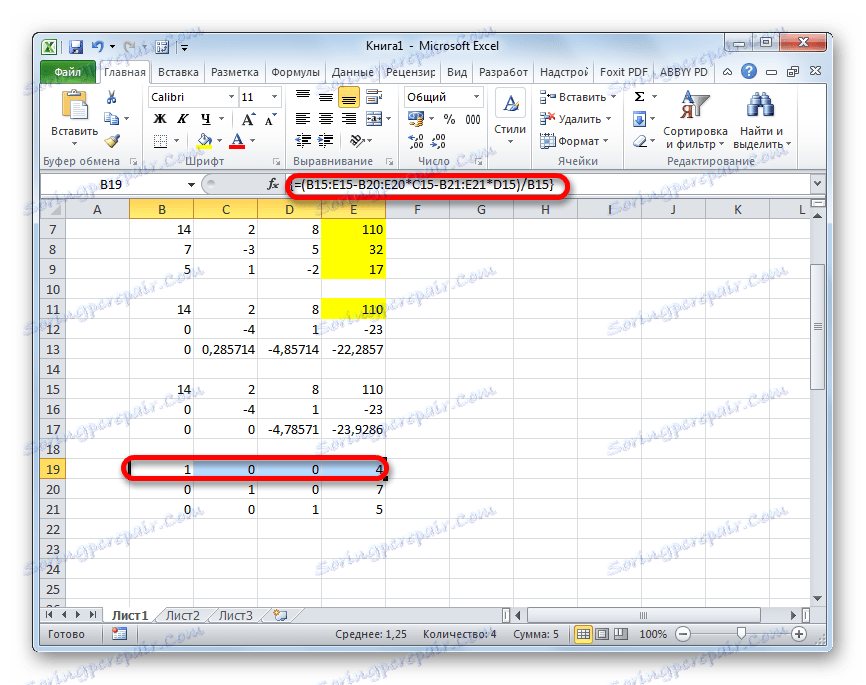
9. Растемо још једну линију. У њега уносимо формулу низа следећег облика:

   =(B15:E15-B20:E20*C15-B21:E21*D15)/B15

   Опет, изаберите целу линију и примените комбинацију тастера Цтрл + Схифт + Ентер .

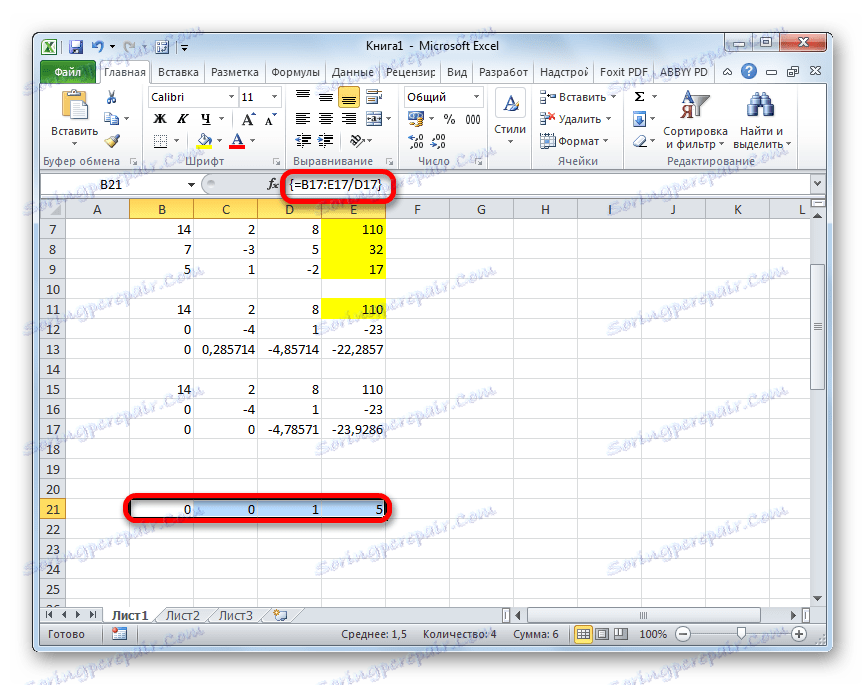
10. Сада погледајте бројеве који су добили у последњој колони последњег блока линија, израчунатих раније. Ови бројеви ( 4 , 7 и 5 ) ће бити корени датог система једначина. Можете то провјерити тако што ћете их замијенити умјесто Кс1 , Кс2 и Кс3 у изразима.

Као што видите, у Екцел систему једначина се може решити низом метода, од којих свака има своје предности и мане. Међутим, сви ови методи могу се условно подијелити на двије велике групе: матрице и помоћу алата за одабир параметара. У неким случајевима, нису увек матричне методе погодне за решавање проблема. Конкретно, када је детерминант матрице нула. У другим случајевима, корисник је слободан да одлучи која опција сматра бољом погодном за себе.

• ← Изградња параболе у ​​Мицрософт Екцелу
• Креирање дугмета у програму Мицрософт Екцел →