Екцел

Израчунавање Лаплаце функције у Мицрософт Екцелу

Једна од најпознатијих не-елементарних функција које се користе у математици, у теорији диференцијалних једначина, у статистици и теорији вероватноће је функција Лапласа. Решавање проблема с њим захтева значајну припрему. Хајде да сазнамо како можете израчунати овај индикатор користећи Екцел алате.

Функција Лаплас

Функција Лаплас има широку практичну и теоријску примену. На пример, често се користи за решавање диференцијалних једначина. Овај израз има још једно еквивалентно име - интеграл вероватноће. У неким случајевима, основа решења је изградња табеле вредности.

Оператор НОРМ.СТ.ДИСТ

У Екцел-у, овај проблем се решава помоћу оператора НОРМ.СТ. РАСП . Његово име је кратица из термина "нормална дистрибуција стандарда". С обзиром да је његов главни задатак да се вратити у додељену ћелију стандардну нормалну интегралну дистрибуцију. Овај оператор припада статистичкој категорији стандардних Екцел функција.

У Екцел 2007 иу ранијим верзијама програма, овај оператер се назива НОРМСДИСТ . Такође се држи компатибилности са савременим верзијама апликација. Али ипак препоручују употребу напреднијег аналогног - НОРМСТ.РАСП .

Синтакса оператора НОРМ.СТ РАСП је следећа:

=НОРМ.СТ.РАСП(z;интегральная)

Застарели оператер НОРМСДИСТ је написан на следећи начин:

=НОРМСТРАСП(z)

Као што видите, у новој варијанти аргументу "Интеграл" додан је постојећем аргументу "З " . Треба напоменути да је сваки аргумент обавезан.

Аргумент "З" означава нумеричку вредност за коју се конструише дистрибуција.

Аргумент "Интеграл" је логична вриједност која може имати "ТРУЕ" ("1") или "ФАЛСЕ" представљање ("0") . У првом случају, функција интегралне дистрибуције се враћа у означену ћелију, ау другом - функцији расподеле тежине.

Решење проблема

Да би извршио потребан прорачун за варијаблу, примјењује се сљедећа формула:

=НОРМ.СТ.РАСП(z;интегральная(1))-0,5

Сада ћемо користити конкретан пример да размотримо употребу оператора НОРМ.СТ РАСП да решимо одређени проблем.

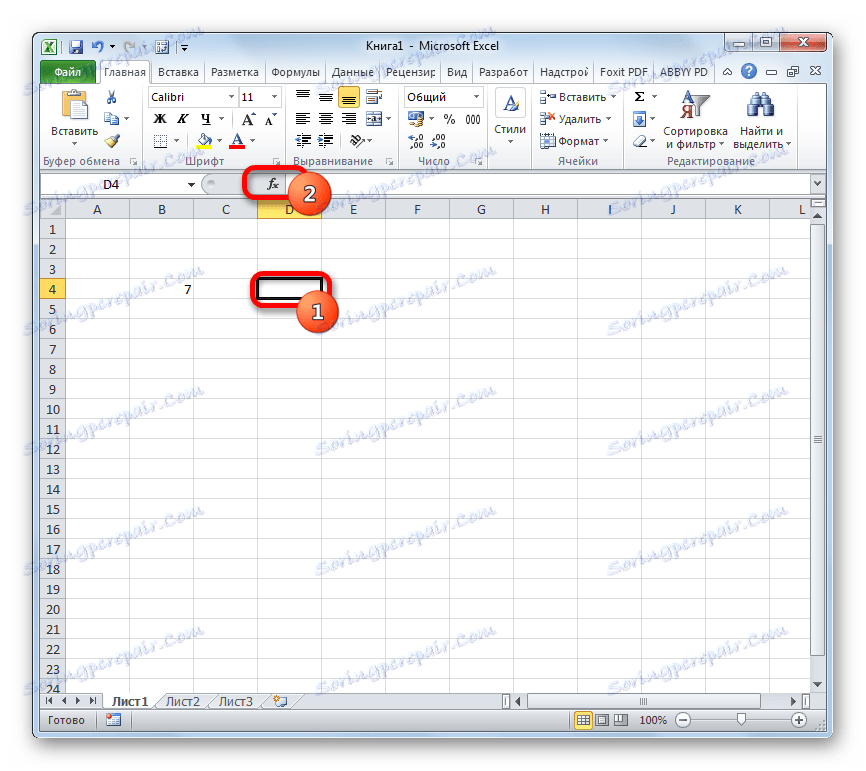
  1. Изаберите ћелију у којој ће се приказати завршени резултат и кликнути на икону "Инсерт фунцтион" , која се налази близу линије формуле.

    2. Идите у Чаробњак за функције у програму Мицрософт Екцел

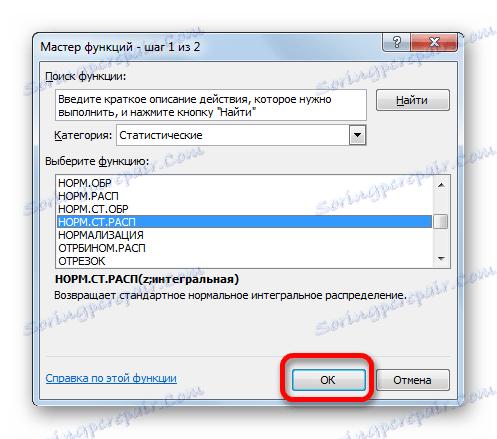
  2. После отварања Чаробњака функције идите у категорију "Статистички" или "Пуну абецедну листу" . Изаберите назив "НОРМ.СТ.РАСП" и кликните на дугме "ОК" .

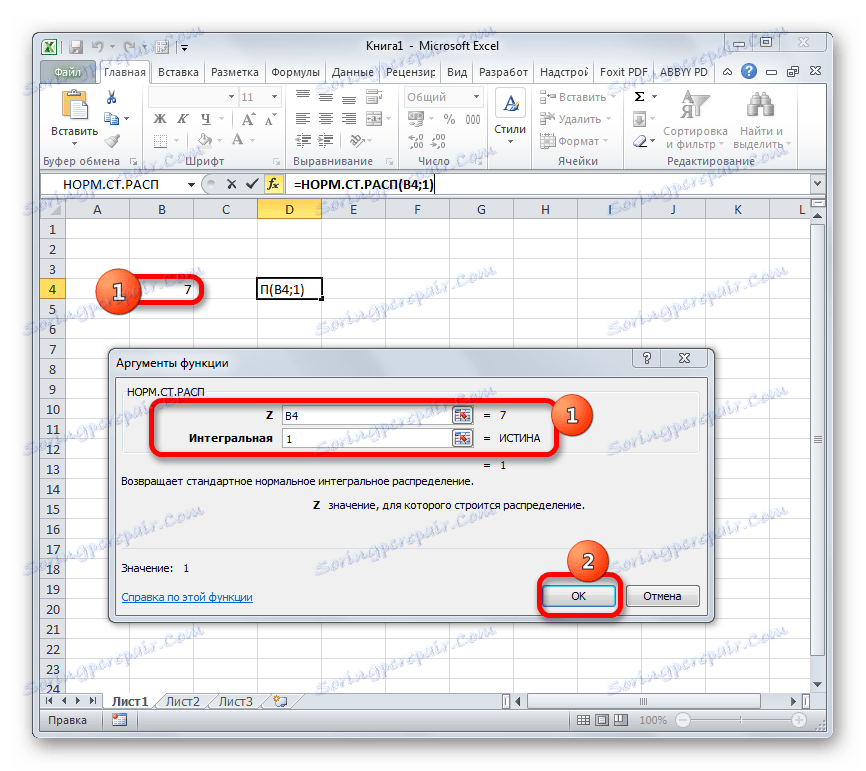
    3. Идите у прозор аргумента НОРМ.СТДИСТ функције у програму Мицрософт Екцел

  3. Активиран је прозор аргумената оператора НОРМ.СТ.РЕСП . У пољу "З" уносимо варијаблу на коју желимо израчунати. Такође, овај аргумент може бити представљен као референца на ћелију која садржи ову варијаблу. У пољу "Интеграл " унесите вредност "1" . То значи да оператер враћа функцију интегралне дистрибуције као рјешење након израчунавања. Након извршених горе наведених корака, кликните на дугме "ОК" .

    4. Прозор аргумента НОРМ.СТДИСТ функције у програму Мицрософт Екцел

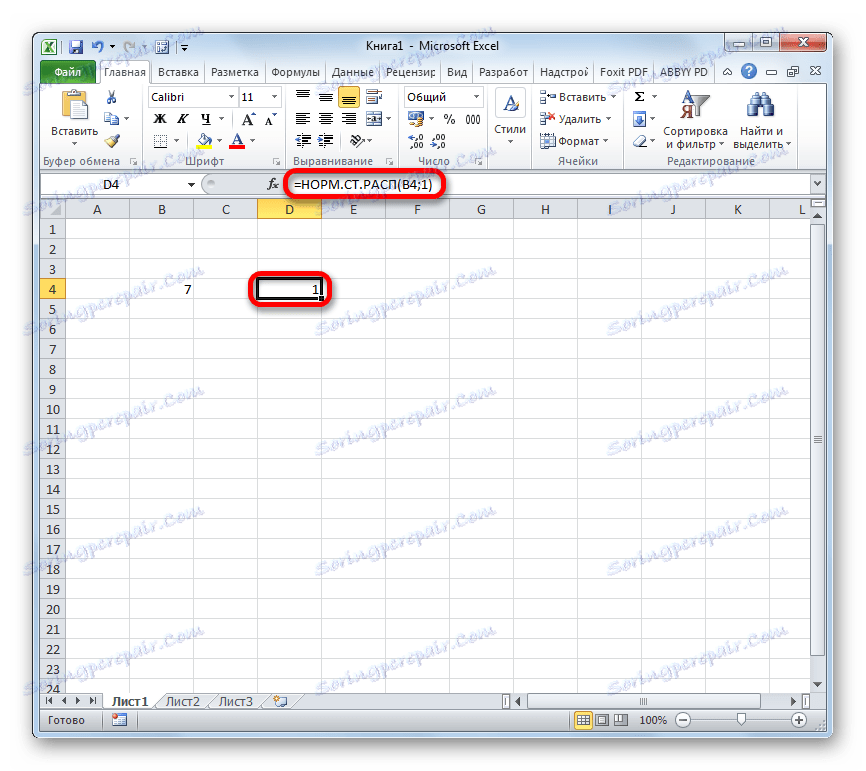
  4. Након тога, резултат обраде података од стране оператора НОРМ.СТ.ДИСТ ће бити приказан у ћелији, што је назначено у првом ставу овог приручника.

    5. Резултат израчунавања функције НОРМ.СТДИСТ у Мицрософт Екцелу

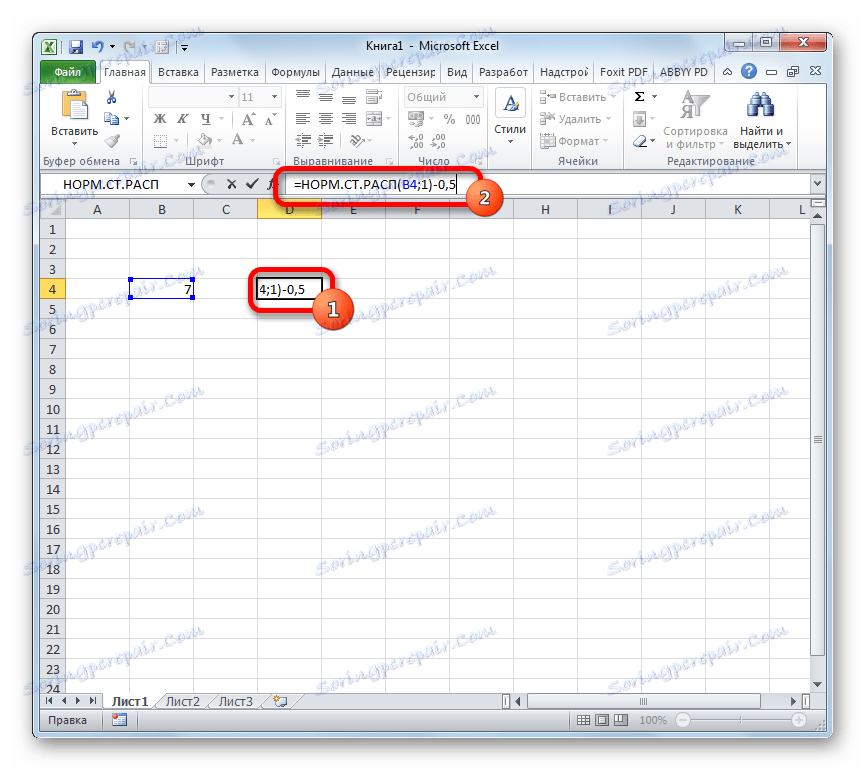
  5. Али то није све. Израчунали смо само стандардну нормалну интегралну расподелу. Да би се израчунала вредност функције Лаплас, потребно је одузети број 0.5 даље од њега. Изаберите ћелију која садржи израз. У линији формуле, након изјаве НОРМ.СТ РАСП, додајте вредност: -0.5 .

    6. Формула за израчунавање функције Лапласа у Мицрософт Екцелу

  6. Да бисте извршили прорачун, притисните тастер Ентер . Резултат је жељена вредност.

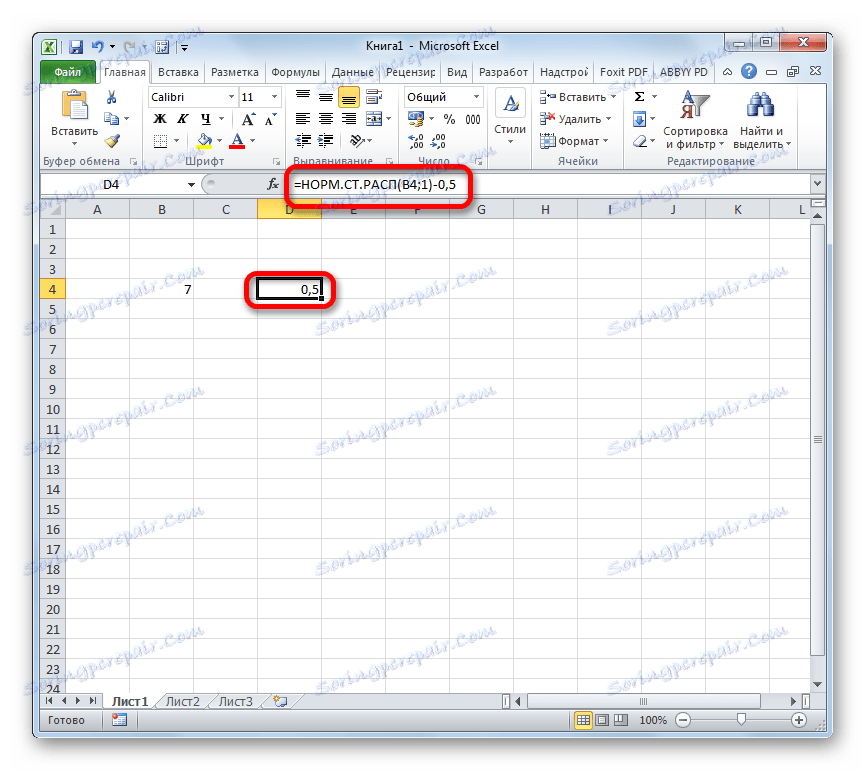
Резултат израчунавања функције Лапласа у Мицрософт Екцелу

Као што видите, није тешко израчунати Лаплацеову функцију за одређену дату нумеричку вредност у програму Екцел. У ове сврхе се користи стандардни оператер НОРМ.СТ.РЕСП .