Примена методе најмањих квадрата у Екцелу
Метода најмањих квадрата је математичка процедура за конструкцију линеарне једначине која би најтачније одговарала сету две серије бројева. Сврха овог метода је да минимизира укупну квадратну грешку. У Екцел-у постоје алати са којима можете да примените ову методу у својим прорачунима. Да видимо како је то учињено.
Садржај
Употреба метода у Екцелу
Метод најмањих квадрата (ОЛС) је математички опис зависности једне променљиве на другом. Може се користити у предвиђању.
Омогућите решење Финд-он Финд Финдер
Да бисте користили ОЛС у Екцел-у, морате омогућити додатак "Финд Солутион" који је подразумевано онемогућен.
- Идите на картицу "Датотека" .
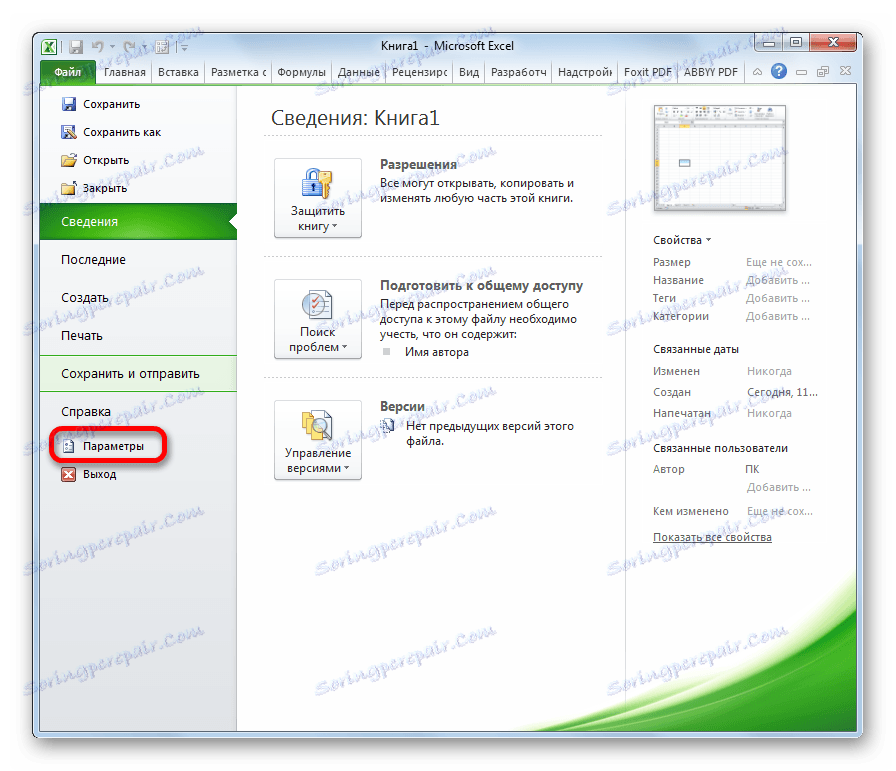
- Кликнемо на име секције "Параметри" .
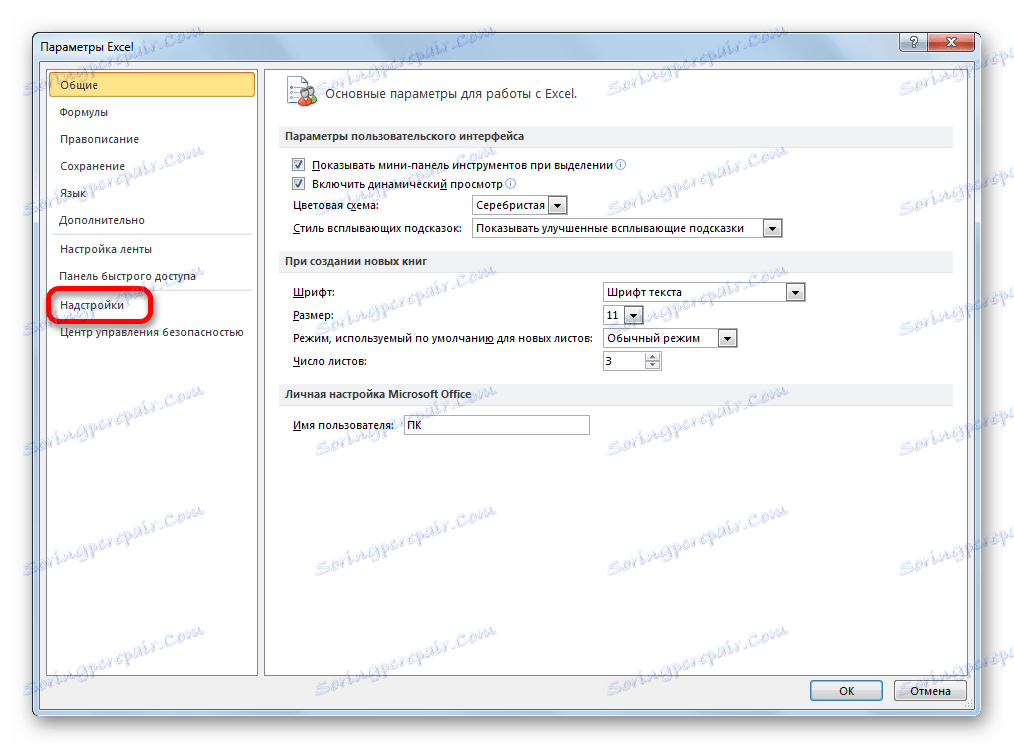
- У прозору који се отвара, ми престанемо да изаберемо пододељак "Додаци" .
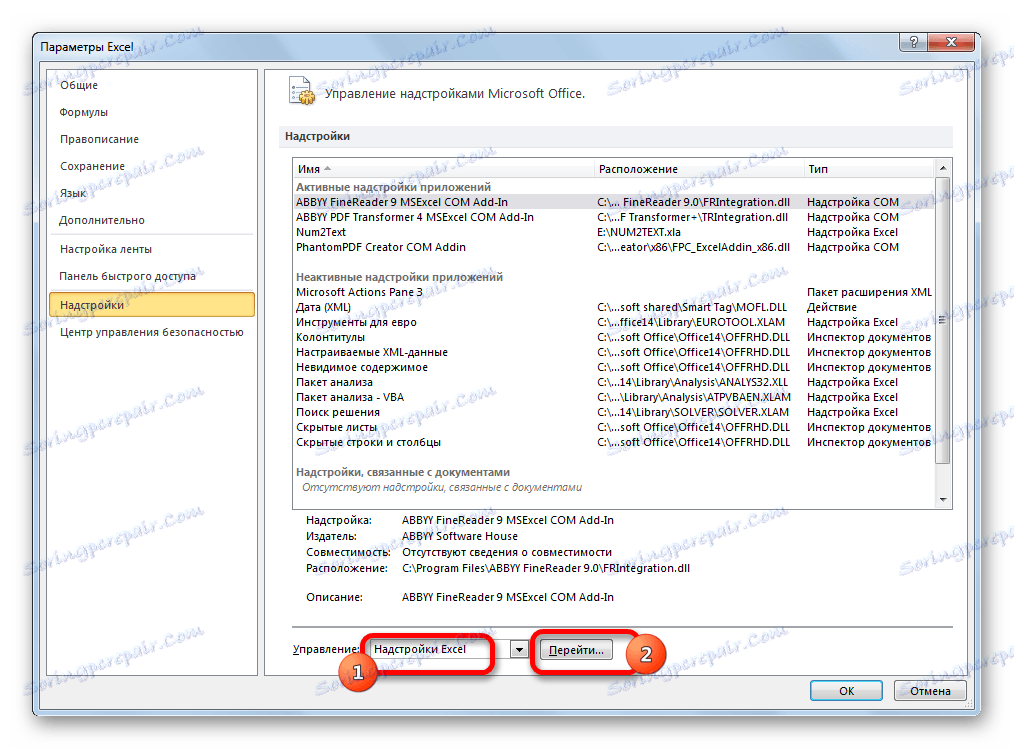
- У оквиру "Управљање" , који се налази на дну прозора, поставите прекидач у положај "Додаци за Екцел" (ако има другачију вредност) и кликните на дугме "Иди ..." .
- Отвара се мали прозор. Ставили смо га у знак за потврду параметра "Проналажење решења" . Кликните на дугме "ОК" .
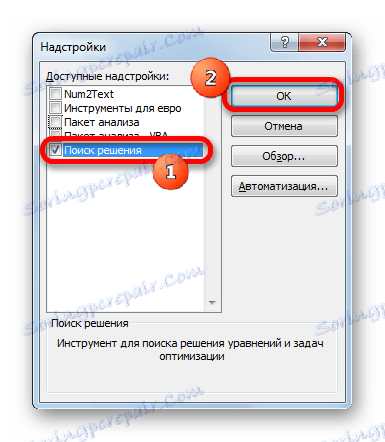
Сада је функција Финд Солутион ин Екцел омогућена, а његови алати се појављују на траци.
Лекција: Претраживање рјешења у програму Екцел
Услови задатака
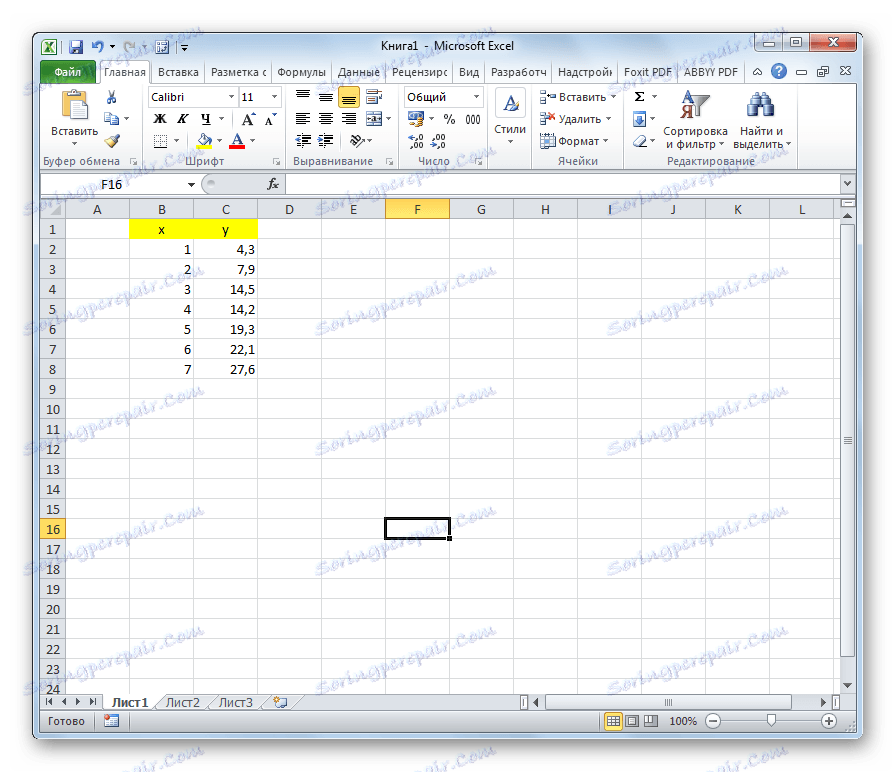
Описимо примену ОЛС-а на конкретном примеру. Имамо два реда бројева к и и , чија је секвенца приказана на слици испод.
Ова функција може прецизније описати ову зависност:
y=a+nx
У овом случају, познато је да је за к = 0, и такође 0 . Дакле, ова једначина може се описати зависношћу и = нк .
Морамо пронаћи минималну суму квадрата разлике.
Решење
Сада ћемо описати директну примену методе.
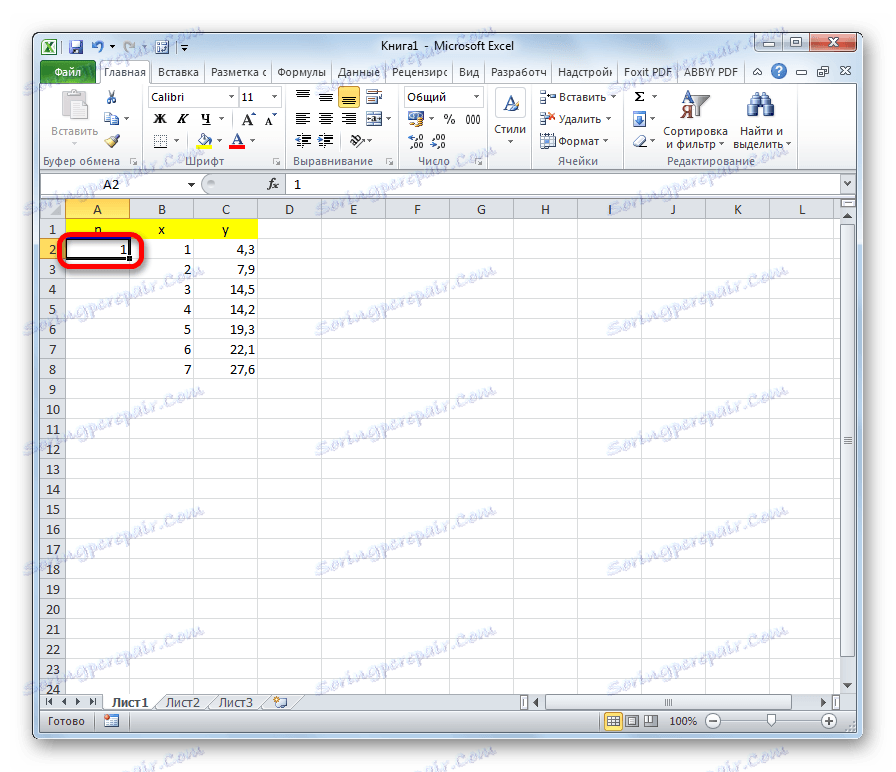
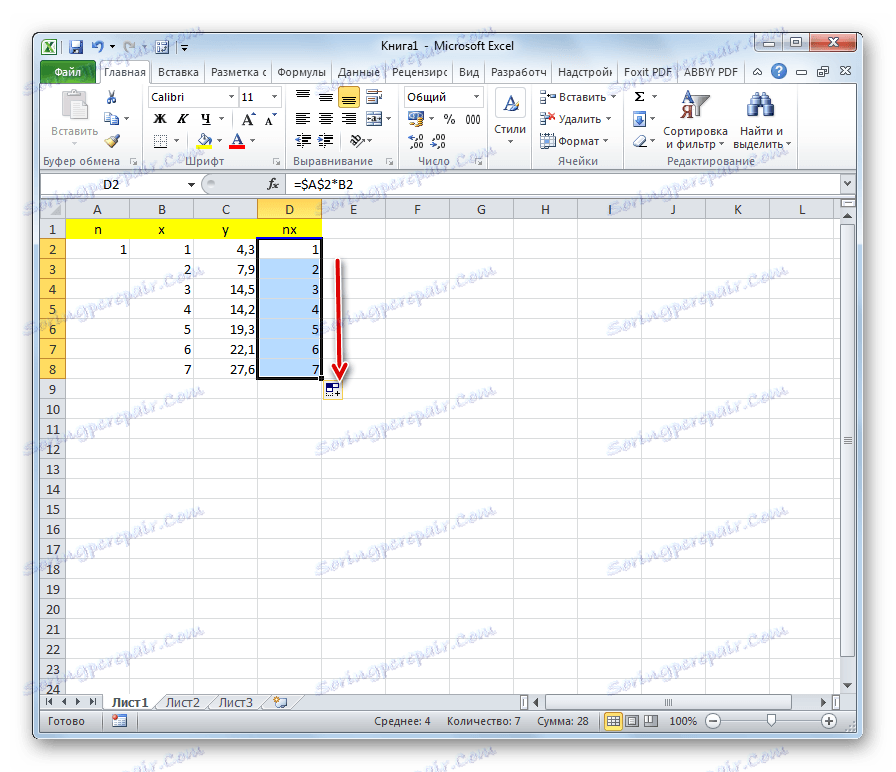
- Лево од прве вредности к ставимо број 1 . Ово је приближна вриједност прве вриједности коефицијента н .
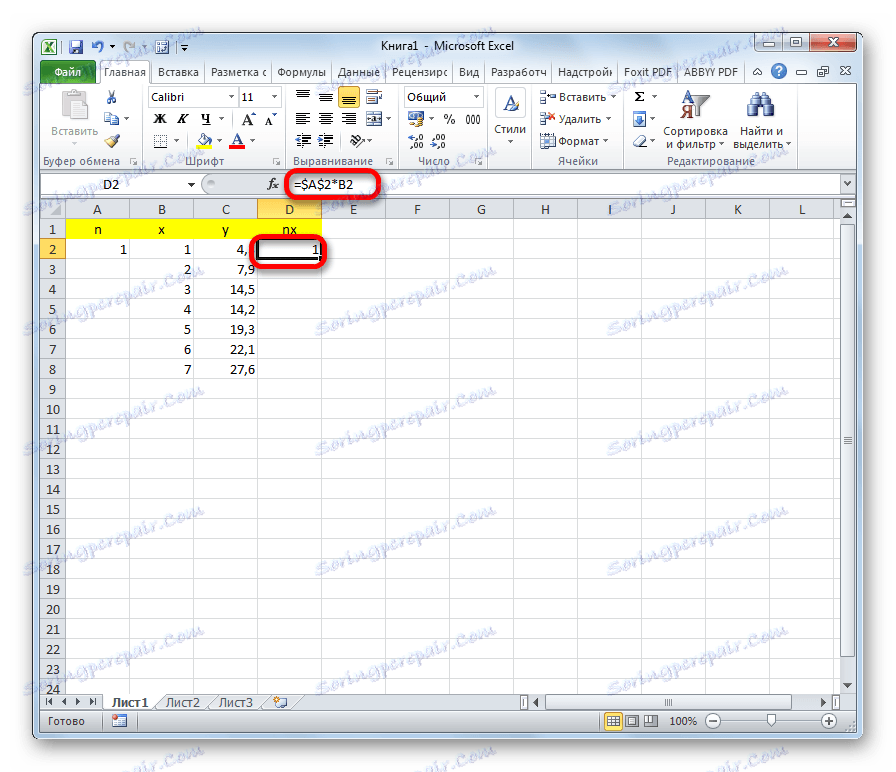
- Десно од колоне и додајте још једну колону - нк . У првој ћелији ове колоне запишемо формулу за множење коефицијента н ћелијом прве варијабле к . Истовремено, врши се веза са пољима са коефицијентом апсолутно , пошто се ова вриједност не мијења. Кликните на дугме Ентер .
- Употреба попуњавање маркера , копирајте ову формулу на цео распон табеле у доњој колони.
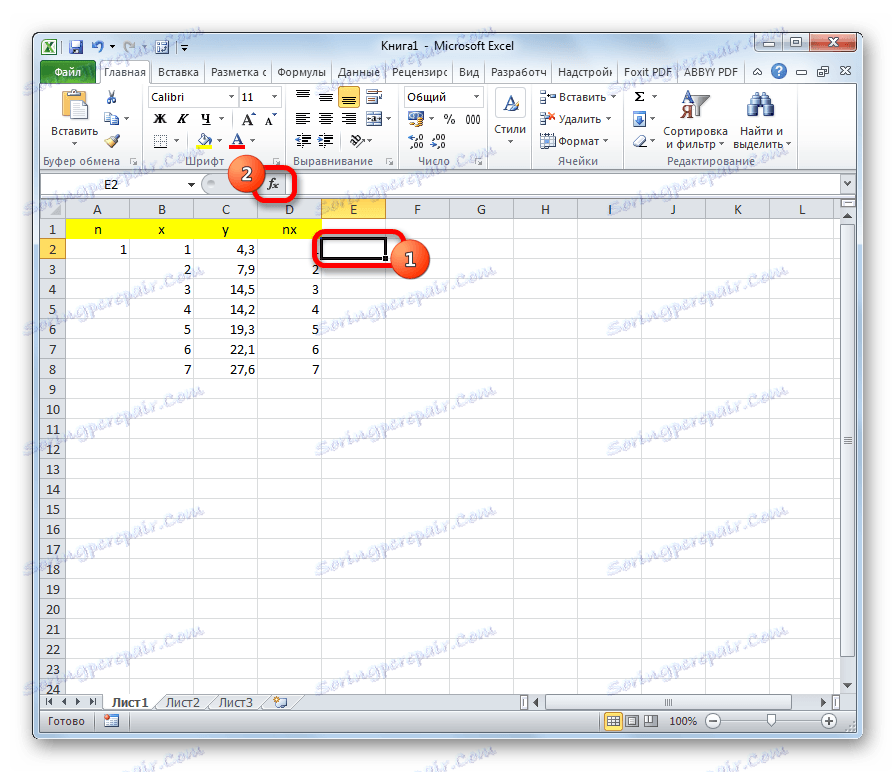
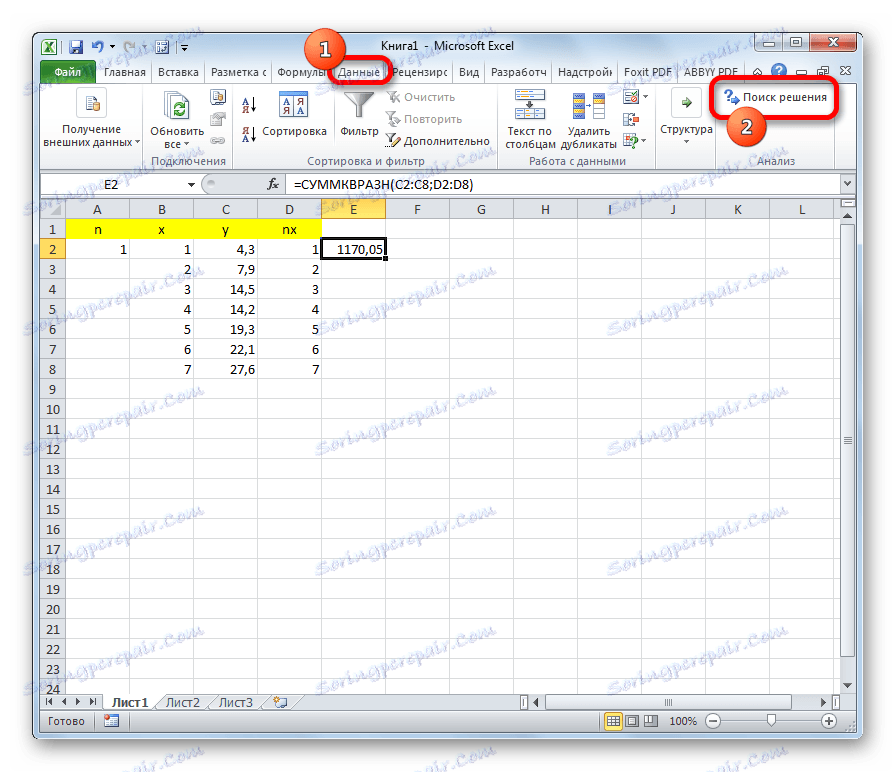
- У одвојеној ћелији израчунајте суму разлика квадратова вредности и и нк . Да бисте то урадили, кликните на дугме "Инсерт фунцтион" .
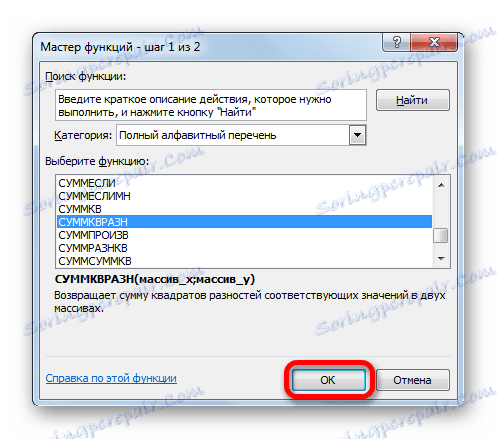
- У отвореном "Чаробњаку функција" тражимо унос "СУММКВРАЗН" . Изаберите је и кликните на дугме "ОК" .
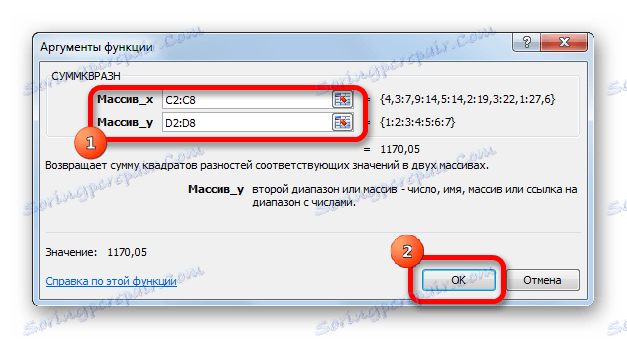
- Отвара прозор аргумената. У пољу "Арраи_к" уносимо опсег ћелија колоне и . У пољу "Арраи_и" уносимо опсег ћелија колоне нк . Да бисте унели вредности, једноставно поставите показивач у поље и изаберите одговарајући распон на листу. Након уноса, кликните на дугме "ОК" .
- Идите на картицу "Подаци" . На траци у алату "Анализа" кликните на дугме "Пронађи решење" .
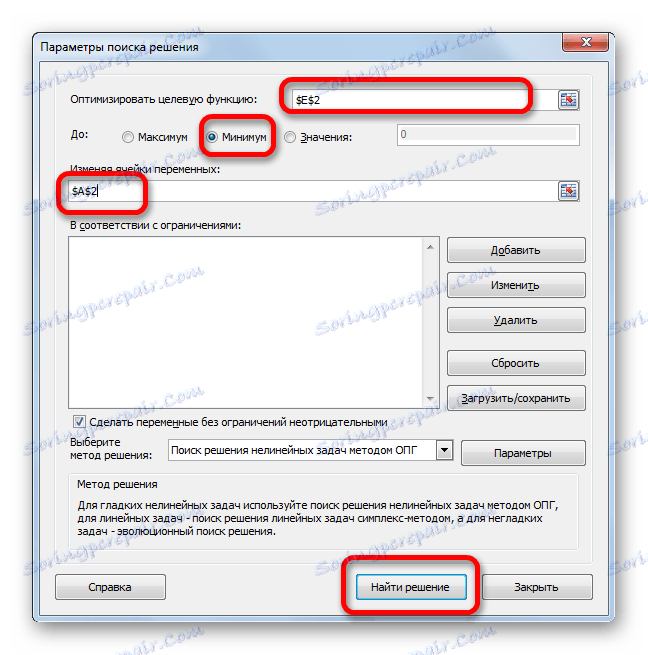
- Отвара се прозор параметара за овај алат. У пољу "Оптимизирам циљну функцију", ми ћемо назначити адресу ћелије са формулом "СУММКВРАЗН" . У параметру "То", потребно је поставити прекидач у положај "Минимум" . У пољу "Промена ћелија" уносимо адресу са вриједношћу коефицијента н . Кликните на дугме "Пронађи рјешење" .
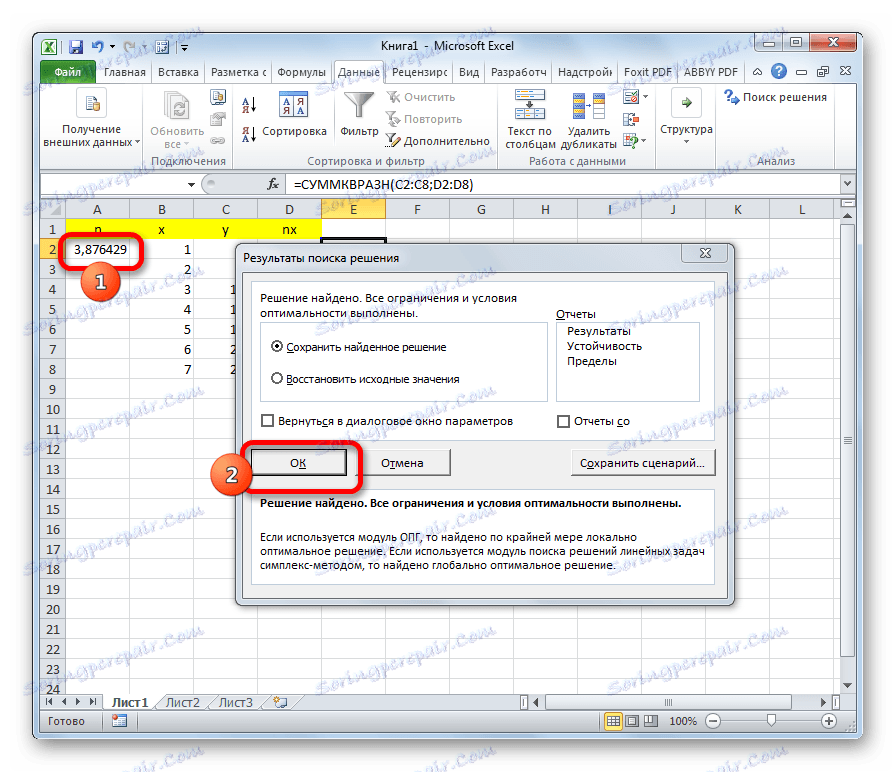
- Решење ће бити приказано у ћелији коефицијента н . Ова вредност ће бити најмањи квадрат функције. Ако резултат задовољава корисника, онда кликните на дугме "ОК" у додатном прозору.
Као што видимо, примена методе најмањих квадрата је прилично сложен математички поступак. Показали смо га у акцији на најједноставнији пример, и има много компликованих случајева. Међутим, Мицрософт Екцел алаткит је дизајниран тако да поједностављује прорачуне што је више могуће.