Решење задатка транспорта у Екцелу

Задатак транспорта је задатак тражења најоптималније варијанте превоза исте врсте робе од добављача према потрошачу. Његова основа је модел који се широко користи у различитим областима математике и економије. У Мицрософт Екцелу постоје алати који у великој мјери олакшавају рјешење задатка транспорта. Сазнаћемо како их користити у пракси.

Садржај

Општи опис задатка транспорта
Алати за решавање проблема са транспортом у Екцелу
Пример решавања транспорта у Екцелу
- Услови задатака
- Решење проблема
Питања и одговори

Општи опис задатка транспорта

Главни циљ задатка транспорта је проналажење оптималног транспортног плана од снабдевача до потрошача са минималним трошковима. Услови таквог проблема пишу се у облику кола или матрице. За Екцел се користи матрични тип.

Ако је укупан обим робе у складиштима добављача једнак вриједности потражње, задатак транспорта се назива затвореним. Ако ови индикатори нису једнаки, такав транспортни задатак се назива отвореним. Да би се то решило, услови треба смањити на затворени тип. Да бисте то урадили, додајте фиктивног продавца или фиктивног купца са акцијама или потребама које су једнаке разлици између понуде и потражње у стварној ситуацији. У овом случају додатна колона или ред са нултим вредностима се додаје у табела трошкова.

Алати за решавање проблема са транспортом у Екцелу

За решавање проблема са транспортом у програму Екцел користи се функција "Финд солутионс" . Проблем је што је подразумевано онемогућен. Да бисте омогућили ову алатку, потребно је извршити одређене радње.

Прелазимо на картицу "Датотека" .

Кликнемо на одељак "Параметри" .

У новом прозору идите на натпис "Додаци" .

У блоку "Управљање" , који се налази на дну отвореног прозора, у падајућој листи зауставићемо избор на ставку "Додаци за Екцел" . Кликните на дугме "Иди ..." .

Покреће се прозор за активирање додатака. Означите поље поред "Проналажење решења" . Кликните на дугме "ОК" .

Због ових радњи, на картици "Подаци" у оквиру поставки "Анализа" на траци појављује се дугме "Пронађи рјешења" . Ово ће нам бити потребно у потрази за решењем проблема са транспортом.

Лекција: Пронађите решење у програму Екцел

Пример решавања транспорта у Екцелу

Сада погледајте конкретан пример решавања проблема саобраћаја.

Услови задатака

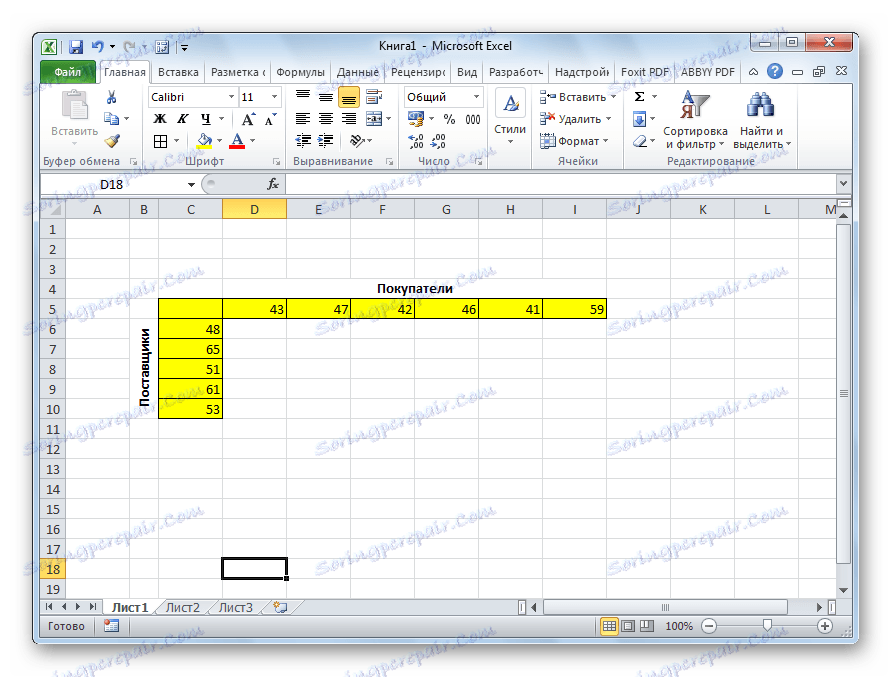
Имамо 5 добављача и 6 купаца. Обим производње ових добављача износи 48, 65, 51, 61, 53 јединице. Потреба купаца: 43, 47, 42, 46, 41, 59 јединица. Дакле, укупан обим снабдевања је једнак вриједности потражње, односно имамо посла затвореног транспорта.

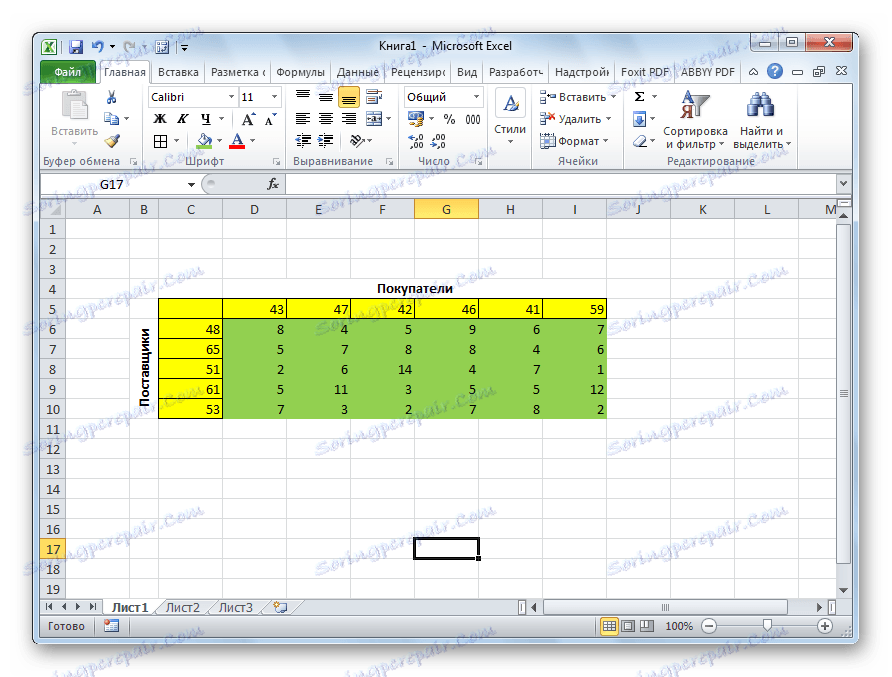
Поред тога, према условима, даје се матрица трошкова транспорта из једне до друге тачке, што је приказано на слици испод у зеленој боји.

Решење проблема

Пред нама је задатак под горе наведеним условима, како би се смањили трошкови транспорта на минимум.

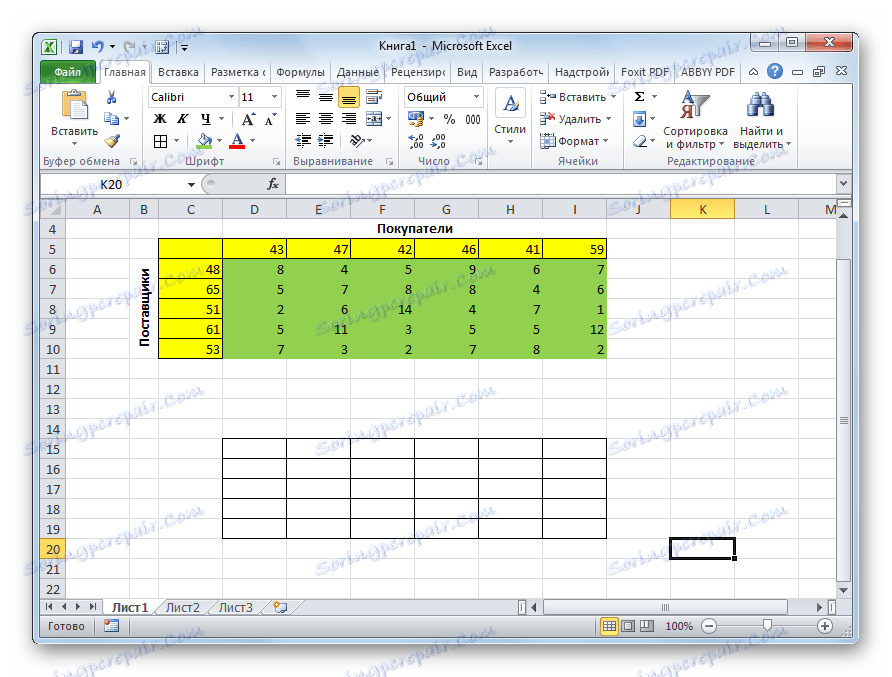
Да бисмо решили проблем, конструишемо табелу са потпуно истим бројем ћелија као што је већ описана матрица трошкова.

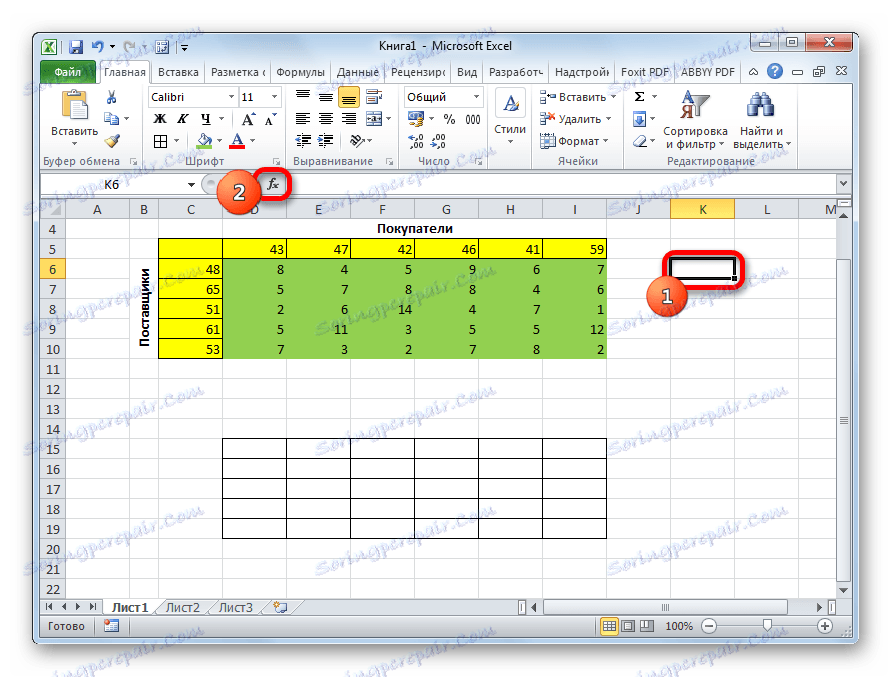
Изаберите било коју празну ћелију на листу. Кликните на икону "Инсерт фунцтион" , која се налази лево од линије формуле.

Отвара се "Чаробњак за функције". На листи коју он предлаже, требало би да нађемо функцију СУМПРОДУЦТ . Изаберите је и кликните на дугме "ОК" .

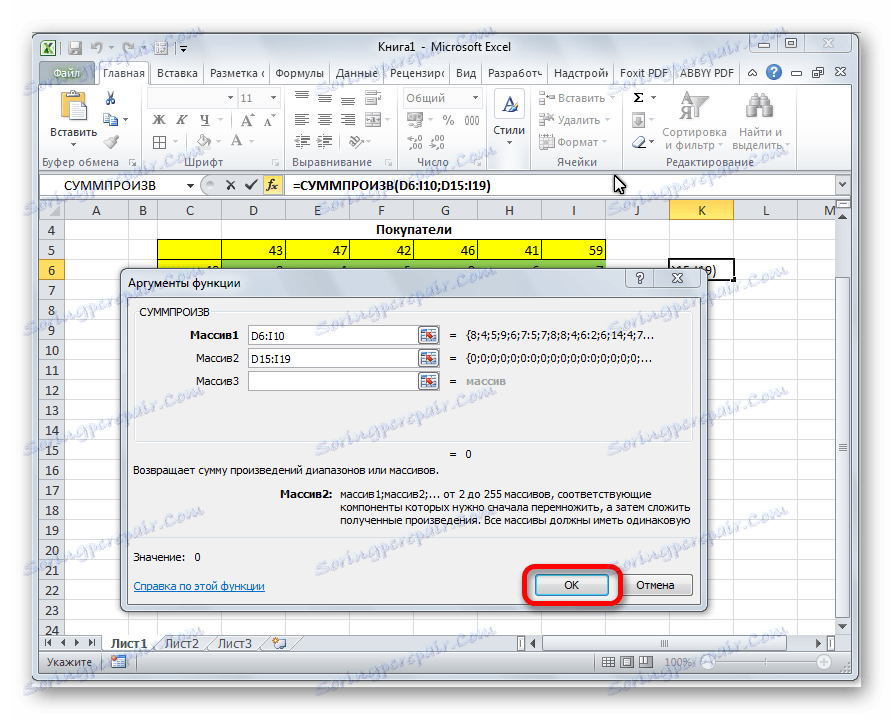
Отвара прозор за унос функције СУМПРОСЕ . Као први аргумент представљамо распон ћелија у матрици трошкова. Да бисте то урадили, довољно је означити податке ћелије помоћу курсора. Други аргумент је опсег ћелија у табели која је припремљена за израчунавање. Затим кликните на дугме "ОК" .

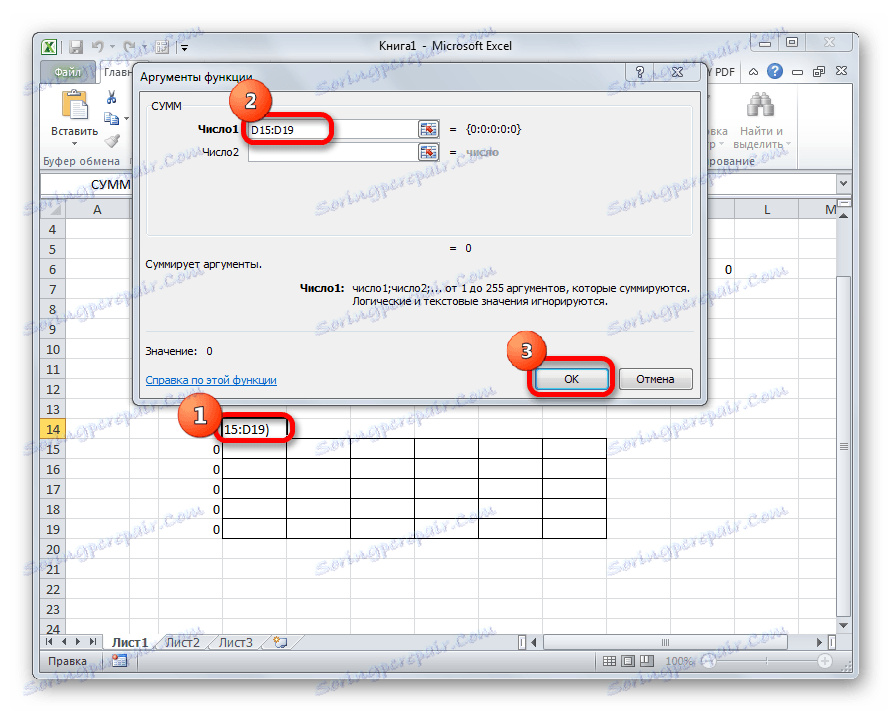
Кликните на ћелију која се налази лево од горње леве ћелије табеле за израчунавање. Као и посљедњи пут када зовемо Фунцтион Визард, отворимо аргументе функције СУМ у њему. Кликом на поље првог аргумента изаберите цео горњи ред ћелија таблице за израчунавање. Након што се њихове координате унесу у одговарајуће поље, кликните на дугме "ОК" .

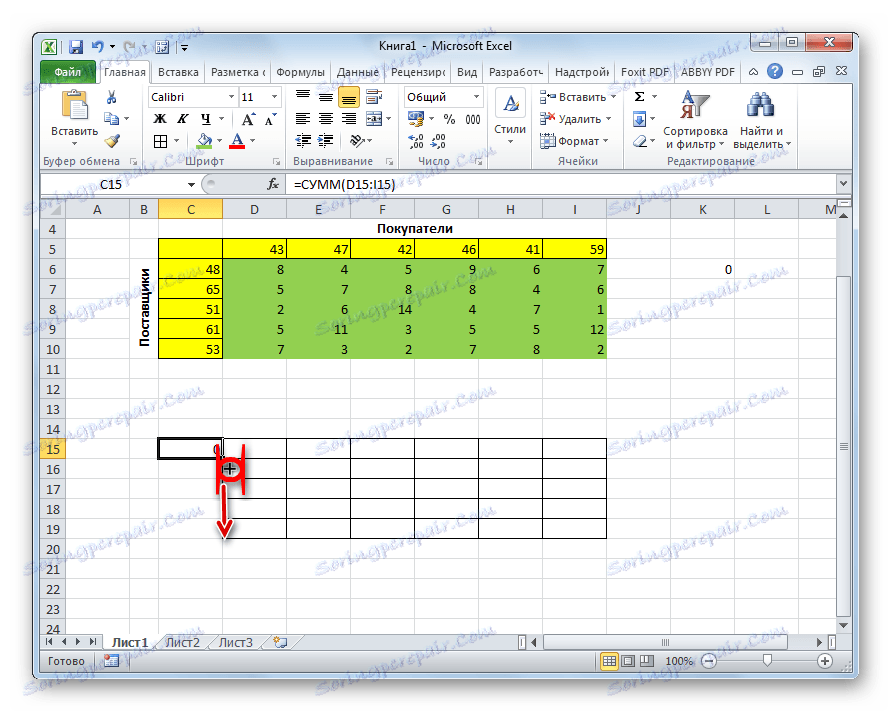
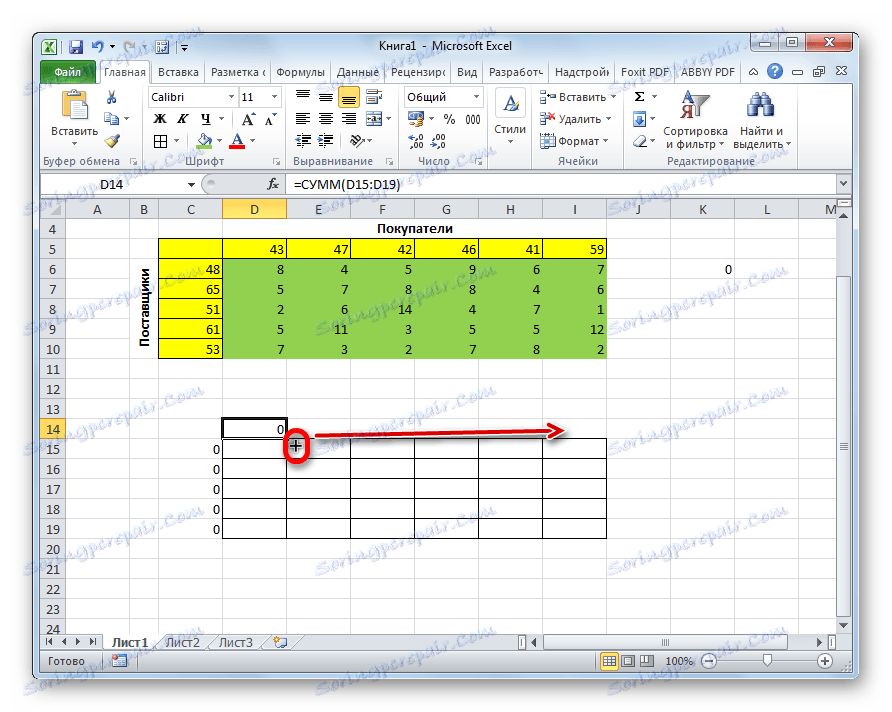
Постајемо у доњем десном углу ћелије са функцијом СУМ . Појављује се ручица за пуњење. Кликните на леви тастер миша и повуците ручицу за пуњење до краја табеле да бисте израчунали. Дакле, копирали смо формулу.

Кликнете на ћелију изнад горње леве ћелије табеле за израчунавање. Као и претходни пут, позивамо функцију СУМ , али овај пут користимо прву колону табеле за израчунавање као аргумент. Кликните на дугме "ОК" .

Копирајте токен за пуњење у формулу за цео ред.

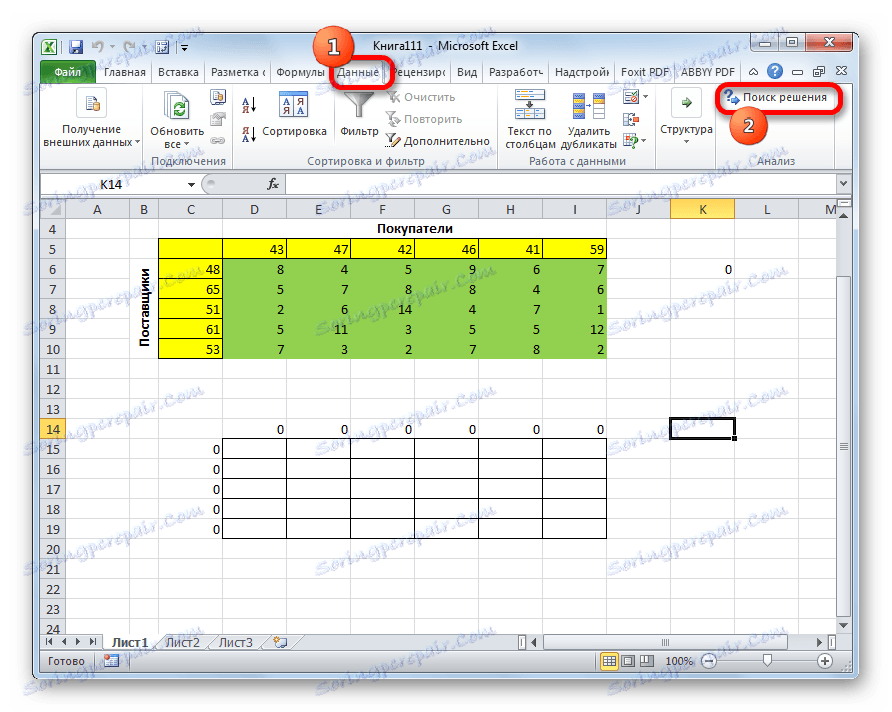
Идите на картицу "Подаци" . У пољу за анализу "Анализа" кликните на дугме "Пронађи решење" .

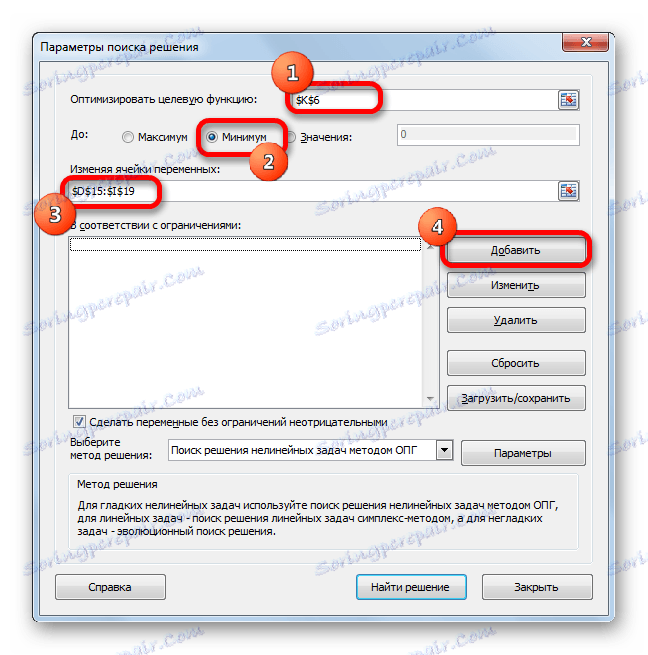
Приказују се опције претраживања за решење. У пољу "Оптимизирајте циљну функцију" наведите ћелију која садржи функцију СУМПРОДУЦТ . У блоку "То" поставите вредност на "Минимум" . У пољу "Промјена ћелија варијабли" дефинишемо цео распон табеле за прорачун. У оквиру поставки "У складу са ограничењима" кликните на дугме "Додај" да бисте додали неколико важних ограничења.

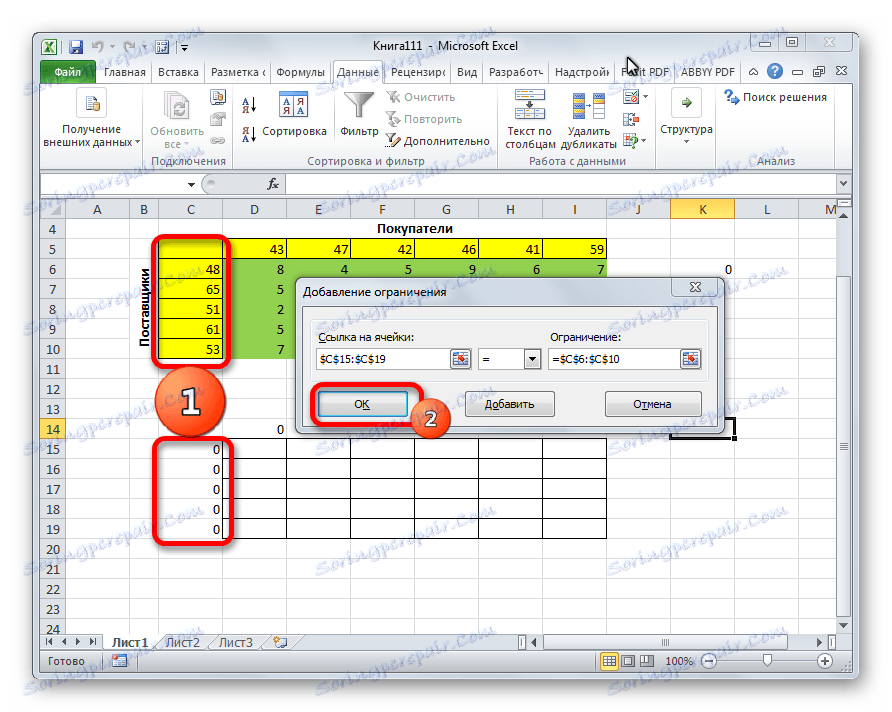
Покреће се прозор за додавање ограничења. Прије свега, морамо додати услов да збир података у редовима табеле за обрачуне треба да буде једнак збиру података у редовима табеле са условима. У пољу "Референца ћелије" наведите опсег суме у редовима табеле рачунања. Затим подесите знак једнакости (=). У пољу "Лимит" наведите распон сума у редовима табеле са условима. Након тога, кликните на дугме "ОК" .

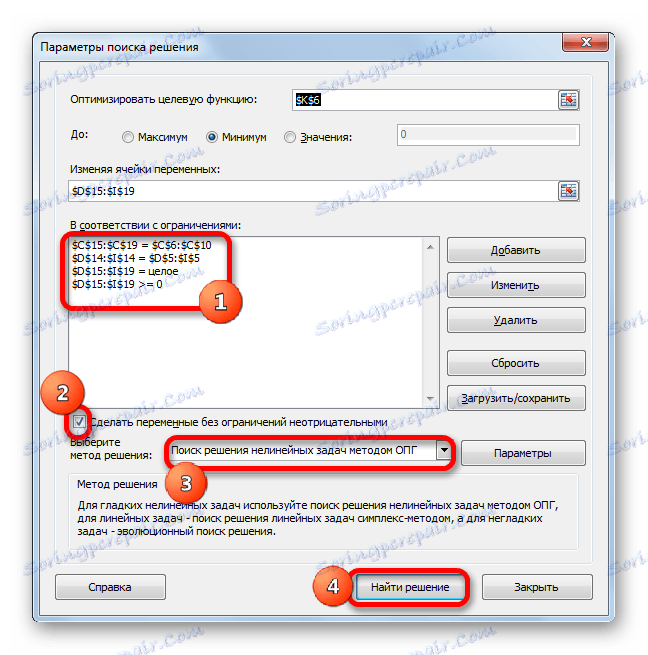
Слично томе, додамо услов да су колоне две табеле једнаке једна другој. Додамо ограничење да би збир опсега свих ћелија у табели за прорачун требало да буде већи или једнак 0, као и услов да то мора бити цео број. Општи поглед на ограничења треба да буде као што је приказано на слици испод. Обавезно проверите да ли у близини ставке "Направите варијабле без ограничења ненективно" постојао је знак за чекање, а метод рјешења је био "Тражење рјешења нелинеарних проблема ОПГ методом" . Након што су сва подешавања наведена, кликните на дугме "Финд Солутион" .

Након тога се обрачун врши. Подаци се изводе у ћелије таблице за обрачун. Приказује се прозор резултата претраге. Ако су резултати задовољавајући, кликните на дугме "ОК" .